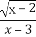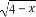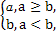题目内容
已知函数f(x)=3ax2+2bx+c,a+b+c=0,且f(0)·f(1)>0.
(1)求证:-2< <-1.
<-1.
(2)若x1,x2是方程f(x)=0的两个实根,求|x1-x2|的取值范围.
(1)见解析 (2) [ ,
,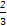 )
)
【解析】(1)当a=0时,f(0)=c,f(1)=2b+c,
又b+c=0,
则f(0)·f(1)=c(2b+c)=-c2<0与已知矛盾.
因而a≠0,则f(0)·f(1)=c(3a+2b+c)
=-(a+b)(2a+b)>0,
即( +1)(
+1)( +2)<0,从而-2<
+2)<0,从而-2< <-1.
<-1.
(2)x1,x2是方程f(x)=0的两个实根,
则x1+x2=- ,x1x2=-
,x1x2=-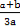 ,
,
那么(x1-x2)2=(x1+x2)2-4x1x2
=(- )2+4×
)2+4×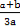 =
=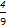 ·(
·( )2+
)2+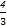 ·
· +
+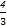
=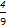 (
( +
+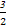 )2+
)2+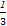 .
.
∵-2< <-1,
<-1,
∴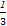 ≤(x1-x2)2<
≤(x1-x2)2<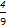 ,
,
∴ ≤|x1-x2|<
≤|x1-x2|<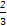 .
.
即|x1-x2|的取值范围是[ ,
,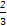 ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目