题目内容
已知斜率为1的直线l与双曲线C: (a>0,b>0)相交于B、D两点,且BD的中点为M(1,3)。
(a>0,b>0)相交于B、D两点,且BD的中点为M(1,3)。
(1)求C的离心率;
(2)设C的右顶点为A,右焦点为F,|DF|·|BF|=17,证明:过A、B、D三点的圆与x轴相切。
 (a>0,b>0)相交于B、D两点,且BD的中点为M(1,3)。
(a>0,b>0)相交于B、D两点,且BD的中点为M(1,3)。(1)求C的离心率;
(2)设C的右顶点为A,右焦点为F,|DF|·|BF|=17,证明:过A、B、D三点的圆与x轴相切。
解:(1)由题设知,l的方程为y=x+2,代人C的方程,并化简,得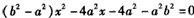
设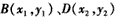
则 ①
①
由M(1,3)为BD的中点知
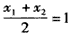 ,故
,故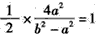 ,即
,即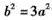 ②
②
故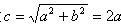
所以C的离心率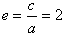 ;
;
(2)由①、②知,C的方程为3x2-y2=3a2,
A(a,0),F(2a,0),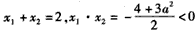
故不妨设x1≤-a,x2≥a
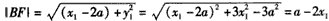
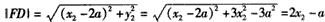
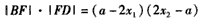
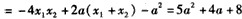
又|BF|·|FD|=17
故5a2+4a+8=17
解得a=1或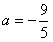 (舍去)
(舍去)
故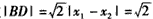
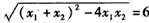
连结MA,则由A(1,0),M(1,3)知|MA|=3,从而MA=MB=MD,且MA⊥x轴,因此以M为圆心,MA为半径的圆经过A、B、D三点,且在点A处与x轴相切,所以过A、B、D三点的圆与x轴相切。
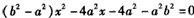
设
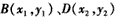
则
 ①
①由M(1,3)为BD的中点知
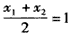 ,故
,故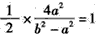 ,即
,即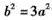 ②
②故
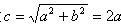
所以C的离心率
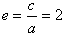 ;
;(2)由①、②知,C的方程为3x2-y2=3a2,
A(a,0),F(2a,0),
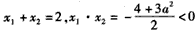
故不妨设x1≤-a,x2≥a
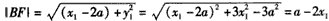
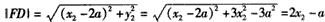
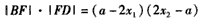
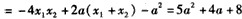
又|BF|·|FD|=17
故5a2+4a+8=17
解得a=1或
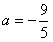 (舍去)
(舍去)故
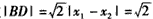
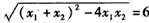
连结MA,则由A(1,0),M(1,3)知|MA|=3,从而MA=MB=MD,且MA⊥x轴,因此以M为圆心,MA为半径的圆经过A、B、D三点,且在点A处与x轴相切,所以过A、B、D三点的圆与x轴相切。

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 已知斜率为1的直线l与双曲线C:
已知斜率为1的直线l与双曲线C: