题目内容

若b＜a＜0，则下列结论不正确的个数是（ ）
①a2＜b2
②ab＜b2
③   
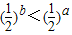
④．
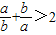A．1个
B．2个
C．3个
D．4个
【答案】分析：利用不等式的基本性质以及特殊值判断选项正误即可．
解答：解：对于①因为b＜a＜0，所以|b|＞|a|，⇒|a|2＞|b|2，?a2＜b2，所以①正确；
②因为b＜a＜0，b＜0，所以ab＜b2，所以②正确；
③因为b＜a＜0，y=，是减函数，所以 不成立，所以③不正确．
④因为b＜a＜0，所以，由基本不等式可知．正确．
错误命题只有③．
故选A．
点评：本题考查不等式的基本性质的应用，函数的单调性以及基本不等式的应用，考查计算能力．
练习册系列答案
相关题目
若b＞a＞0，则下列不等式中一定成立的是（　　）
A、a＞
a+b
2
＞
ab
＞b
B、b＞
ab
＞
a+b
2
＞a
C、b＞
a+b
2
＞
ab
＞a
D、b＞a＞
a+b
2
＞
ab
若b＜a＜0，则下列不等式中正确的是（　　）
A、
1
a
＞
1
b
B、|a|＞|b|
C、
b
a
+
a
b
＞2
D、a+b＞ab
若b＜a＜0，则下列结论不正确的个数是（　　）
①a2＜b2
②ab＜b2
③(
1
2
)b＜(
1
2
)a   
④
a
b
+
b
a
＞2．
若b＜a＜0，则下列结论不正确的是（　　）
若b＜a＜0，则下列不等式中正确的是（ ）
A．＞
B．|a|＞|b|
C．+＞2
D．a+b＞ab

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网