题目内容
本题满分16分)两个数列{an},{bn},满足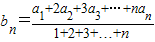 .★(参考公式
.★(参考公式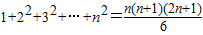 )
)求证:{bn}为等差数列的充要条件是{an}为等差数列.
【答案】分析:由条件可得 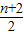 bn+1-
bn+1-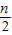 bn=an+1 ,
bn=an+1 , bn-
bn-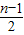 bn-1=an,相减可得 an+1 -an═
bn-1=an,相减可得 an+1 -an═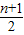 (bn+1-bn )+
(bn+1-bn )+ (bn+1-bn )-
(bn+1-bn )-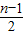 (bn-bn-1),由于{bn}为等差数列的充要条件是 bn+1-bn=bn-bn-1=常数d,此时an+1 -an=
(bn-bn-1),由于{bn}为等差数列的充要条件是 bn+1-bn=bn-bn-1=常数d,此时an+1 -an=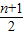 d+
d+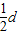 -
-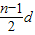 =
=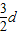 ,是个常数,从而结论成立.
,是个常数,从而结论成立.
解答:证明:∵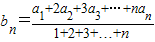 ,∴bn+1=
,∴bn+1=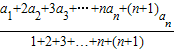 ,
,
∴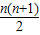 bn=a1+2a2+3a3+…+nan ①,
bn=a1+2a2+3a3+…+nan ①,
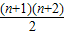 bn+1=a1+2a2+3a3+…+nan+(n+1)an+1.②
bn+1=a1+2a2+3a3+…+nan+(n+1)an+1.②
②减去①可得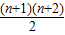 bn+1-
bn+1-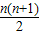 bn=(n+1)an+1.
bn=(n+1)an+1.
两边同时除以n+1可得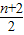 bn+1-
bn+1-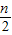 bn=an+1 ③,
bn=an+1 ③,
∴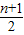 bn-
bn-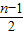 bn-1=an ④.
bn-1=an ④.
③减去④可得 an+1 -an=(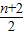 bn+1 -
bn+1 -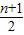 bn )-(
bn )-(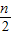 bn -
bn -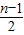 bn-1 )
bn-1 )
=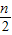 bn+1 +bn+1 -
bn+1 +bn+1 -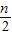 bn-
bn- bn-
bn-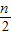 bn+
bn+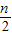 bn-1-
bn-1- bn-1
bn-1
=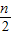 (bn+1-bn )+
(bn+1-bn )+ (bn+1-bn )+
(bn+1-bn )+ (bn-bn-1)-
(bn-bn-1)-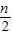 (bn-bn-1)
(bn-bn-1)
=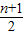 (bn+1-bn )+
(bn+1-bn )+ (bn+1-bn )-
(bn+1-bn )-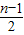 (bn-bn-1).
(bn-bn-1).
由于{bn}为等差数列的充要条件是 bn+1-bn=bn-bn-1=常数d,
此时an+1 -an=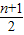 d+
d+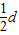 -
-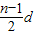 =
=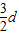 ,是个常数.
,是个常数.
故:{bn}为等差数列的充要条件是{an}为等差数列.
点评:本题主要考查用分析法和综合法证明数学命题,体现了等价转化的数学思想,属于中档题.
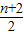 bn+1-
bn+1-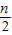 bn=an+1 ,
bn=an+1 , bn-
bn-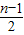 bn-1=an,相减可得 an+1 -an═
bn-1=an,相减可得 an+1 -an═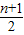 (bn+1-bn )+
(bn+1-bn )+ (bn+1-bn )-
(bn+1-bn )-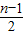 (bn-bn-1),由于{bn}为等差数列的充要条件是 bn+1-bn=bn-bn-1=常数d,此时an+1 -an=
(bn-bn-1),由于{bn}为等差数列的充要条件是 bn+1-bn=bn-bn-1=常数d,此时an+1 -an=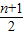 d+
d+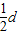 -
-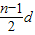 =
=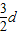 ,是个常数,从而结论成立.
,是个常数,从而结论成立.解答:证明:∵
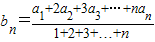 ,∴bn+1=
,∴bn+1=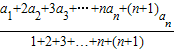 ,
,∴
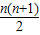 bn=a1+2a2+3a3+…+nan ①,
bn=a1+2a2+3a3+…+nan ①,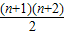 bn+1=a1+2a2+3a3+…+nan+(n+1)an+1.②
bn+1=a1+2a2+3a3+…+nan+(n+1)an+1.②②减去①可得
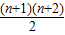 bn+1-
bn+1-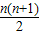 bn=(n+1)an+1.
bn=(n+1)an+1.两边同时除以n+1可得
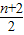 bn+1-
bn+1-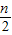 bn=an+1 ③,
bn=an+1 ③,∴
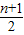 bn-
bn-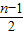 bn-1=an ④.
bn-1=an ④.③减去④可得 an+1 -an=(
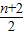 bn+1 -
bn+1 -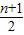 bn )-(
bn )-(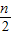 bn -
bn -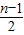 bn-1 )
bn-1 )=
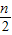 bn+1 +bn+1 -
bn+1 +bn+1 -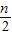 bn-
bn- bn-
bn-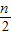 bn+
bn+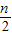 bn-1-
bn-1- bn-1
bn-1 =
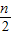 (bn+1-bn )+
(bn+1-bn )+ (bn+1-bn )+
(bn+1-bn )+ (bn-bn-1)-
(bn-bn-1)-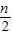 (bn-bn-1)
(bn-bn-1)=
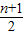 (bn+1-bn )+
(bn+1-bn )+ (bn+1-bn )-
(bn+1-bn )-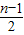 (bn-bn-1).
(bn-bn-1).由于{bn}为等差数列的充要条件是 bn+1-bn=bn-bn-1=常数d,
此时an+1 -an=
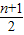 d+
d+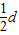 -
-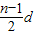 =
=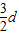 ,是个常数.
,是个常数.故:{bn}为等差数列的充要条件是{an}为等差数列.
点评:本题主要考查用分析法和综合法证明数学命题,体现了等价转化的数学思想,属于中档题.

练习册系列答案
相关题目
 为实数,且
为实数,且
 的解;
的解; ,
,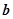 满足
满足 ,试写出
,试写出 .
.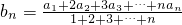 .★(参考公式
.★(参考公式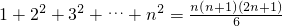 )
)