题目内容
本题满分16分)两个数列{an},{bn},满足bn=
.★(参考公式1+22+32+…+n2=
)
求证:{bn}为等差数列的充要条件是{an}为等差数列.
| a1+2a2+3a3+…+nan |
| 1+2+3+…+n |
| n(n+1)(2n+1) |
| 6 |
求证:{bn}为等差数列的充要条件是{an}为等差数列.
证明:∵bn=
,∴bn+1=
,
∴
bn=a1+2a2+3a3+…+nan ①,
bn+1=a1+2a2+3a3+…+nan+(n+1)an+1.②
②减去①可得
bn+1-
bn=(n+1)an+1.
两边同时除以n+1可得
bn+1-
bn=an+1 ③,
∴
bn-
bn-1=an ④.
③减去④可得 an+1 -an=(
bn+1 -
bn )-(
bn -
bn-1 )
=
bn+1 +bn+1 -
bn-
bn-
bn+
bn-1-
bn-1
=
(bn+1-bn )+
(bn+1-bn )+
(bn-bn-1)-
(bn-bn-1)
=
(bn+1-bn )+
(bn+1-bn )-
(bn-bn-1).
由于{bn}为等差数列的充要条件是 bn+1-bn=bn-bn-1=常数d,
此时an+1 -an=
d+
d-
d=
d,是个常数.
故:{bn}为等差数列的充要条件是{an}为等差数列.
| a1+2a2+3a3+…+nan |
| 1+2+3+…+n |
| a1+2a2+3a3+…+nan+(n+1)an |
| 1+2+3+…+n+(n+1) |
∴
| n(n+1) |
| 2 |
| (n+1)(n+2) |
| 2 |
②减去①可得
| (n+1)(n+2) |
| 2 |
| n(n+1) |
| 2 |
两边同时除以n+1可得
| n+2 |
| 2 |
| n |
| 2 |
∴
| n+1 |
| 2 |
| n-1 |
| 2 |
③减去④可得 an+1 -an=(
| n+2 |
| 2 |
| n+1 |
| 2 |
| n |
| 2 |
| n-1 |
| 2 |
=
| n |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
=
| n |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
=
| n+1 |
| 2 |
| 1 |
| 2 |
| n-1 |
| 2 |
由于{bn}为等差数列的充要条件是 bn+1-bn=bn-bn-1=常数d,
此时an+1 -an=
| n+1 |
| 2 |
| 1 |
| 2 |
| n-1 |
| 2 |
| 3 |
| 2 |
故:{bn}为等差数列的充要条件是{an}为等差数列.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 为实数,且
为实数,且
 的解;
的解; ,
,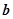 满足
满足 ,试写出
,试写出 .
.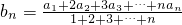 .★(参考公式
.★(参考公式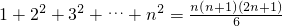 )
)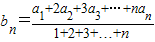 .★(参考公式
.★(参考公式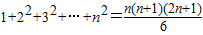 )
)