题目内容
如图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③.图③ 中直线AM与x轴交于点N(n,0),设f(m)=n.
中直线AM与x轴交于点N(n,0),设f(m)=n.
给出下列命题:
①f(
)=0;
②f(x)是偶函数;
③f(x)在定义域上单调递增;
④f(x)的图象关于点(
,0)对称
则下列命题的正确的是( )
 中直线AM与x轴交于点N(n,0),设f(m)=n.
中直线AM与x轴交于点N(n,0),设f(m)=n.给出下列命题:
①f(
| 1 |
| 2 |
②f(x)是偶函数;
③f(x)在定义域上单调递增;
④f(x)的图象关于点(
| 1 |
| 2 |
则下列命题的正确的是( )
分析:先弄清楚由区间(0,1)到实数集R的映射过程,并画出如图所示的图象,进而可判断出答案.
解答: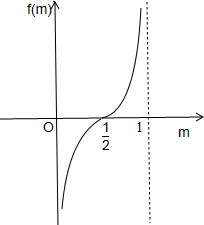 解:根据映射规则,画出如图所示的图象.
解:根据映射规则,画出如图所示的图象.
①当m=
时,点M在y轴上,此时AM在y轴上,直线AM与x轴交于点N(0,0),∴f(
)=0,故①正确;
②∵m的取值范围是(0,1),关于原点不对称,故不是偶函数,因此②不正确;
③其对应规则是:m从0到1逐渐增大时,f(m)依次从-∞到+∞逐渐增大,故f(x)在定义域上单调递增,因此③正确;
④由图3可知:圆上的点M与M′关于y轴对称时,f(m)与f(m′)在x轴上对应的点N与N′也关于原点对称,即f(x)的图象关于点(
,0)对称.
故选C.
 解:根据映射规则,画出如图所示的图象.
解:根据映射规则,画出如图所示的图象.①当m=
| 1 |
| 2 |
| 1 |
| 2 |
②∵m的取值范围是(0,1),关于原点不对称,故不是偶函数,因此②不正确;
③其对应规则是:m从0到1逐渐增大时,f(m)依次从-∞到+∞逐渐增大,故f(x)在定义域上单调递增,因此③正确;
④由图3可知:圆上的点M与M′关于y轴对称时,f(m)与f(m′)在x轴上对应的点N与N′也关于原点对称,即f(x)的图象关于点(
| 1 |
| 2 |
故选C.
点评:正确理解给出的映射规则及画出图象是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 10、如图展示了一个由区间(0,4)到实数集R的映射过程:区间(0,4)中的实数m对应数轴上的点M(如图),将线段AB围成一个正方形,使两端点A、B恰好重合(如图),再将这个正方形放在平面直角坐标系中,使其中两个顶点在y轴上,点A的坐标为(0,4)(如图),若图中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.现给出以下命题:
10、如图展示了一个由区间(0,4)到实数集R的映射过程:区间(0,4)中的实数m对应数轴上的点M(如图),将线段AB围成一个正方形,使两端点A、B恰好重合(如图),再将这个正方形放在平面直角坐标系中,使其中两个顶点在y轴上,点A的坐标为(0,4)(如图),若图中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.现给出以下命题:


