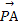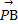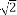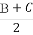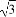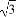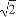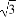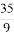Question

在平面直角坐标系中,已知向量a=(-1,2),又点A(8,0),B(n,t),C(ksinθ,t)(0≤θ≤).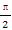

(1)若⊥a,且||=|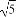|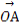(O为坐标原点),求向量.

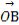(2)若向量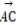与向量a共线,当k>4,且tsinθ取最大值4时,求·.

 

Answer 1

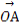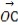(1) 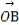=(24,8)或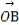=(-8,-8) (2) 32

【解析】(1)可得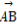=(n-8,t),

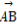∵⊥a,∴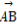·a=(n-8,t)·(-1,2)=0,

得n=2t+8,则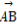=(2t,t).

又|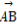|=|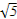|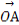,||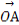=8.

∴(2t)2+t2=5×64,解得t=±8,

当t=8时,n=24;当t=-8时,n=-8.

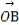∴=(24,8)或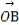=(-8,-8).

(2)∵向量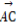与向量a共线,

∴t=-2ksinθ+16,

tsinθ=(-2ksinθ+16)sinθ

=-2k(sinθ-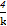)2+.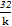

∵k>4,∴0<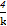<1,故当sinθ=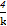时,tsinθ取最大值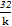,有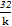=4,得k=8.

这时,sinθ=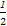,k=8,tsinθ=4,得t=8,

则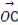=(4,8),

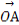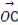∴·=(8,0)·(4,8)=32.