题目内容
已知|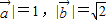 ,且
,且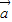 与
与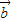 的夹角为θ.
的夹角为θ.(1)若θ=
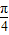 ,求
,求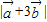 ;
;(2)若
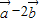 与
与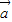 垂直,求cosθ.
垂直,求cosθ.
【答案】分析:(1) 先求出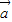 •
•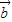 的值,代入|
的值,代入|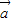 +3
+3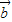 |=
|=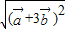 的式子进行运算.
的式子进行运算.
(2) 由(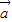 -2
-2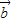 )⊥
)⊥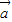 ,可得(
,可得( 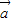 -2
-2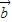 )•
)•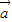 =0,解出
=0,解出 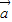 •
•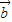 =
= ,再利用两个向量的数量积的定义求出cosθ 的值.
,再利用两个向量的数量积的定义求出cosθ 的值.
解答:解:(1)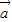 •
•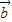 =|
=|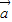 |•|
|•|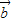 |•cos
|•cos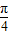 =1×
=1×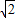 ×
×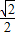 =1,
=1,
|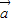 +3
+3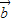 |=
|=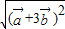 =
=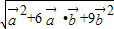 =
=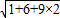 =5.
=5.
(2)∵(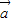 -2
-2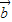 )⊥
)⊥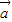 ,∴(
,∴( 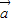 -2
-2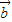 )•
)•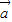 =
=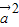 -2
-2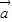
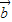 =1-2
=1-2 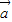
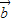 =0,
=0,
∴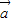
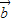 =
= =|
=|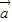 |•|
|•|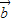 |cosθ=1×
|cosθ=1×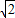 cosθ,∴cosθ=
cosθ,∴cosθ=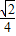 .
.
点评:本题考查两个向量的数量积的定义,向量的模的求法,两个香辣ing垂直的性质.
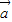 •
•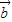 的值,代入|
的值,代入|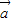 +3
+3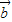 |=
|=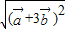 的式子进行运算.
的式子进行运算.(2) 由(
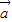 -2
-2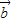 )⊥
)⊥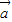 ,可得(
,可得( 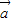 -2
-2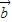 )•
)•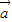 =0,解出
=0,解出 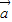 •
•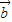 =
= ,再利用两个向量的数量积的定义求出cosθ 的值.
,再利用两个向量的数量积的定义求出cosθ 的值.解答:解:(1)
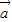 •
•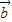 =|
=|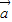 |•|
|•|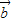 |•cos
|•cos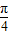 =1×
=1×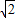 ×
×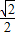 =1,
=1,|
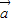 +3
+3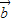 |=
|=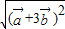 =
=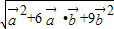 =
=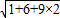 =5.
=5.(2)∵(
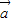 -2
-2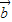 )⊥
)⊥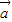 ,∴(
,∴( 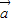 -2
-2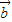 )•
)•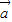 =
=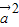 -2
-2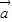
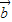 =1-2
=1-2 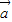
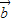 =0,
=0,∴
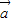
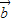 =
= =|
=|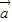 |•|
|•|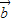 |cosθ=1×
|cosθ=1×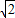 cosθ,∴cosθ=
cosθ,∴cosθ=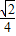 .
.点评:本题考查两个向量的数量积的定义,向量的模的求法,两个香辣ing垂直的性质.

练习册系列答案
相关题目
 ,
, ,且
,且 与
与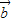 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( ) ,
, ,且
,且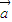 与
与 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( ) ,
,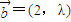 ,且
,且 与
与 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( )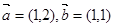 ,且
,且 与
与 的夹角为锐角,则实数
的夹角为锐角,则实数 的取值范围是______.
的取值范围是______. ,
, ,且
,且 与
与 的夹角为锐角,则实数
的夹角为锐角,则实数 的取值范围是__.
的取值范围是__.