题目内容
已知 ,
,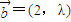 ,且
,且 与
与 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( )A.(-∞,1)
B.(0,1)
C.(1,+∞)
D.(-∞,-4)∪(-4,1)
【答案】分析:由 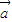 与
与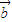 的夹角为锐角,设为θ,则 0<cosθ<1,由两个向量的夹角公式求出cosθ的解析式,代入不等式求解.
的夹角为锐角,设为θ,则 0<cosθ<1,由两个向量的夹角公式求出cosθ的解析式,代入不等式求解.
解答:解:∵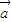 与
与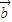 的夹角为锐角,设为θ,
的夹角为锐角,设为θ,
则 0<cosθ<1,
又cosθ=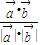 =
=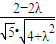 ,
,
∴0<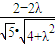 <1,
<1,
∴λ<1 且4-8λ+4λ2<20+5λ2,
即 λ<1 且λ≠-4,
故选 D.
点评:本题考查两个向量的夹角公式,当两个向量的夹角为锐角时,夹角的余弦值大于0且小于.
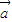 与
与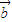 的夹角为锐角,设为θ,则 0<cosθ<1,由两个向量的夹角公式求出cosθ的解析式,代入不等式求解.
的夹角为锐角,设为θ,则 0<cosθ<1,由两个向量的夹角公式求出cosθ的解析式,代入不等式求解.解答:解:∵
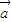 与
与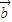 的夹角为锐角,设为θ,
的夹角为锐角,设为θ,则 0<cosθ<1,
又cosθ=
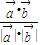 =
=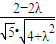 ,
,∴0<
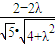 <1,
<1,∴λ<1 且4-8λ+4λ2<20+5λ2,
即 λ<1 且λ≠-4,
故选 D.
点评:本题考查两个向量的夹角公式,当两个向量的夹角为锐角时,夹角的余弦值大于0且小于.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 ,
, ,且
,且 与
与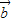 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( ) ,
, ,且
,且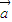 与
与 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( )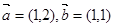 ,且
,且 与
与 的夹角为锐角,则实数
的夹角为锐角,则实数 的取值范围是______.
的取值范围是______. ,
, ,且
,且 与
与 的夹角为锐角,则实数
的夹角为锐角,则实数 的取值范围是__.
的取值范围是__.