题目内容
设函数 R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x).(1)若a=f'(2),b=f'(1),c=f'(0),求a、b、c的值;
(2)在(1)的条件下,记
 ,求证:F(1)+F(2)+F(3)+…+F(n)<
,求证:F(1)+F(2)+F(3)+…+F(n)< N*);
N*);(3)设关于x的方程f'(x)=0的两个实数根为α、β,且1<α<β<2.试问:是否存在正整数n,使得
 ?说明理由.
?说明理由.
【答案】分析:(1)求出f'(x)=x2+ax+b,由 a=f'(2),b=f'(1),c=f'(0),求出a=-1,b=c=-3.
(2)根据 ,F(1)和 F(2)都小于
,F(1)和 F(2)都小于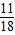 ,且F(1)+F(2)=0,当n≥3时,F(n)<
,且F(1)+F(2)=0,当n≥3时,F(n)<
 (
( ),用放缩法证明F(1)+F(2)+F(3)+…+F(n)<
),用放缩法证明F(1)+F(2)+F(3)+…+F(n)<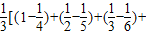 …+
…+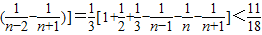 <
<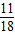 .
.
(3)根据 f'(1)•f'(2)=(1-α)(1-β)(2-α)(2-β)=(α-1)(2-α)(β-1)(2-β )≤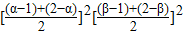 =
=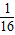 ,可得
,可得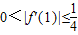 ,或
,或 ,故存在n=1或2,
,故存在n=1或2,
使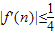 .
.
解答:解:(1)f'(x)=x2+ax+b,由已知可得a=-1,b=c=-3.…(4分)
(2) ,
,
当n=1时, ;当n=2时,
;当n=2时,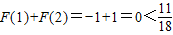 ;
;
当n≥3时,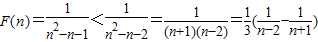 .
.
所以F(1)+F(2)+F(3)+…+F(n)<F(1)+F(2)+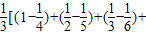 …+
…+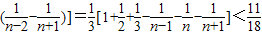
= (1+
(1+ +
+ -
-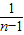 -
-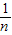 -
- )<
)< (1+
(1+ +
+ )=
)=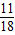 ,
,
所以F(1)+F(2)+F(3)+…+F(n)< N*).…(9分)
N*).…(9分)
(3)根据题设,可令f'(x)=(x-α)(x-β).
∴f'(1)•f'(2)=(1-α)(1-β)(2-α)(2-β)
=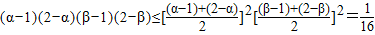 ,
,
∴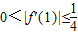 ,或
,或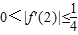 ,所以存在n=1或2,使
,所以存在n=1或2,使 .…(13分).
.…(13分).
点评:本题考查用放缩法、数学归纳法证明不等式,基本不等式的应用,是一道难题.
(2)根据
 ,F(1)和 F(2)都小于
,F(1)和 F(2)都小于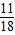 ,且F(1)+F(2)=0,当n≥3时,F(n)<
,且F(1)+F(2)=0,当n≥3时,F(n)< (
( ),用放缩法证明F(1)+F(2)+F(3)+…+F(n)<
),用放缩法证明F(1)+F(2)+F(3)+…+F(n)<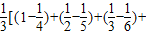 …+
…+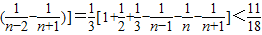 <
<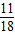 .
.(3)根据 f'(1)•f'(2)=(1-α)(1-β)(2-α)(2-β)=(α-1)(2-α)(β-1)(2-β )≤
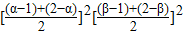 =
=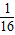 ,可得
,可得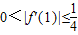 ,或
,或 ,故存在n=1或2,
,故存在n=1或2,使
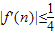 .
.解答:解:(1)f'(x)=x2+ax+b,由已知可得a=-1,b=c=-3.…(4分)
(2)
 ,
,当n=1时,
 ;当n=2时,
;当n=2时,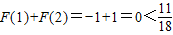 ;
;当n≥3时,
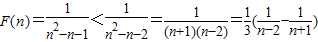 .
.所以F(1)+F(2)+F(3)+…+F(n)<F(1)+F(2)+
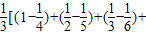 …+
…+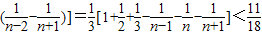
=
 (1+
(1+ +
+ -
-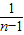 -
-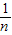 -
- )<
)< (1+
(1+ +
+ )=
)=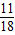 ,
,所以F(1)+F(2)+F(3)+…+F(n)<
 N*).…(9分)
N*).…(9分)(3)根据题设,可令f'(x)=(x-α)(x-β).
∴f'(1)•f'(2)=(1-α)(1-β)(2-α)(2-β)
=
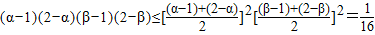 ,
,∴
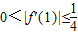 ,或
,或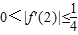 ,所以存在n=1或2,使
,所以存在n=1或2,使 .…(13分).
.…(13分).点评:本题考查用放缩法、数学归纳法证明不等式,基本不等式的应用,是一道难题.

练习册系列答案
相关题目
 R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x). ,
, N*);
N*); ?说明理由.
?说明理由. R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x). ,求证:F(1)+F(2)+F(3)+…+F(n)<
,求证:F(1)+F(2)+F(3)+…+F(n)< N*);
N*); ?说明理由.
?说明理由. R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x). ,求证:F(1)+F(2)+F(3)+…+F(n)<
,求证:F(1)+F(2)+F(3)+…+F(n)< N*);
N*); ?说明理由.
?说明理由. R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x). ,求证:F(1)+F(2)+F(3)+…+F(n)<
,求证:F(1)+F(2)+F(3)+…+F(n)< N*);
N*); ?说明理由.
?说明理由.