题目内容
设函数 R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x).
(1)若a=f'(2),b=f'(1),c=f'(0),求a、b、c的值;
(2)在(1)的条件下,记 ,求证:F(1)+F(2)+F(3)+…+F(n)<
,求证:F(1)+F(2)+F(3)+…+F(n)< N*);
N*);
(3)设关于x的方程f'(x)=0的两个实数根为α、β,且1<α<β<2.试问:是否存在正整数n0,使得 ?说明理由.
?说明理由.
 R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x).(1)若a=f'(2),b=f'(1),c=f'(0),求a、b、c的值;
(2)在(1)的条件下,记
 ,求证:F(1)+F(2)+F(3)+…+F(n)<
,求证:F(1)+F(2)+F(3)+…+F(n)< N*);
N*);(3)设关于x的方程f'(x)=0的两个实数根为α、β,且1<α<β<2.试问:是否存在正整数n0,使得
 ?说明理由.
?说明理由.解:(1)f'(x)=x2+ax+b,由已知可得a=﹣1,b=c=﹣3
(2) ,
,
当n=1时,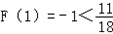 ;
;
当n=2时, ;
;
当n≧3时,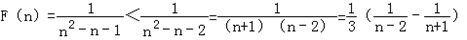 .
.
所以F(1)+F(2)+F(3)+…+F(n)<
F(1)+F(2)+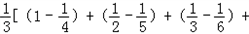 …+
…+
= (1+
(1+ +
+ ﹣
﹣ ﹣
﹣ ﹣
﹣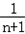 )<
)< (1+
(1+ +
+ )=
)=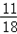 ,
,
所以F(1)+F(2)+F(3)+…+F(n)<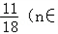 N*).
N*).
(3)根据题设,可令f'(x)=(x﹣α)(x﹣β).
∴f'(1)·f'(2)=(1﹣α)(1﹣β)(2﹣α)(2﹣β)= ,
,
∴ ,或
,或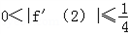 ,
,
所以存在n0=1或2,使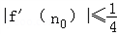 .
.
(2)
 ,
,当n=1时,
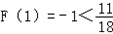 ;
;当n=2时,
 ;
;当n≧3时,
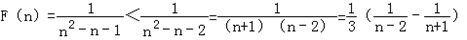 .
.所以F(1)+F(2)+F(3)+…+F(n)<
F(1)+F(2)+
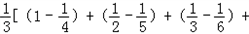 …+
…+
=
 (1+
(1+ +
+ ﹣
﹣ ﹣
﹣ ﹣
﹣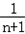 )<
)< (1+
(1+ +
+ )=
)=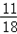 ,
,所以F(1)+F(2)+F(3)+…+F(n)<
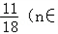 N*).
N*).(3)根据题设,可令f'(x)=(x﹣α)(x﹣β).
∴f'(1)·f'(2)=(1﹣α)(1﹣β)(2﹣α)(2﹣β)=
 ,
,∴
 ,或
,或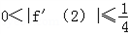 ,
,所以存在n0=1或2,使
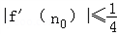 .
.
练习册系列答案
相关题目
 R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x). ,
, N*);
N*); ?说明理由.
?说明理由. R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x). ,求证:F(1)+F(2)+F(3)+…+F(n)<
,求证:F(1)+F(2)+F(3)+…+F(n)< N*);
N*); ?说明理由.
?说明理由. R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x). ,求证:F(1)+F(2)+F(3)+…+F(n)<
,求证:F(1)+F(2)+F(3)+…+F(n)< N*);
N*); ?说明理由.
?说明理由. R),函数f(x)的导数记为f'(x).
R),函数f(x)的导数记为f'(x). ,求证:F(1)+F(2)+F(3)+…+F(n)<
,求证:F(1)+F(2)+F(3)+…+F(n)< N*);
N*); ?说明理由.
?说明理由.