题目内容
【题目】设P为双曲线 
右支上一点，M，N分别是圆（x+4）2+y2=4和（x﹣4）2+y2=1上的点，设|PM|﹣|PN|的最大值和最小值分别为m，n，则|m﹣n|=（ ）
A.4
B.5
C.6
D.7
【答案】C
【解析】解：圆C1：（x+4）2+y2=4的圆心为（﹣4，0），半径为r1=2；
圆C2：（x﹣4）2+y2=1的圆心为（4，0），半径为r2=1，
设双曲线 
的左右焦点为F1（﹣4，0），F2（4，0），
连接PF1，PF2，F1M，F2N，
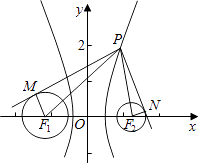
可得|PF1|﹣|PF2|=2是定值，|PM|=|PF1|+r1，
|PN|=（|PF2|﹣r2），所以|PM|﹣|PN|的最大值2a+r1+r2=5，
|PM|=|PF1|﹣r1，
|PN|=（|PF2|+r2），所以|PM|﹣|PN|的最小值：2a﹣r1﹣r2=﹣1．
可得m=5，n=﹣1，则|m﹣n|=6．
故选：C．
【题目】要分析学生初中升学考试的数学成绩对高一年级数学学习有什么影响，在高一年级学生中随机抽取10名学生，分析他们入学的数学成绩(x)和高一年级期末数学考试成绩(y)(如下表)：
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
y | 65 | 78 | 52 | 85 | 92 | 89 | 73 | 98 | 56 | 75 |
（1）画出散点图；
（2）判断入学成绩(x)与高一期末考试成绩(y)是否有线性相关关系；
（3）如果x与y具有线性相关关系，求出回归直线方程；
【题目】某学校在校学生2 000人，为了学生的“德、智、体”全面发展，学校举行了跑步和登山比赛活动，每人都参加而且只参与其中一项比赛，各年级参与比赛的人数情况如下表：
高一年级 | 高二年级 | 高三年级 | |
跑步人数 | a | b | c |
登山人数 | x | y | z |
其中a∶b∶c＝2∶5∶3，全校参与登山的人数占总人数的 
.为了了解学生对本次活动的满意程度，从中抽取一个200人的样本进行调查，则高三年级参与跑步的学生中应抽取( )
A.15人
B.30人
C.40人
D.45人
