题目内容
甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n个白球.现从甲,乙两袋中各任取2个球.
(Ⅰ)若n=3,求取到的4个球全是红球的概率;
(Ⅱ)若取到的4个球中至少有2个红球的概率为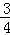 ,求n.
,求n.
(1)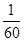 ;(2) 2
;(2) 2
解析试题分析:(1)“取到的4个球全是红球”这个事件就是从甲袋取两个球都是红球和从乙袋取两个球都是红球同时发生,其概率是两个事件发生的概率的乘积,因此概率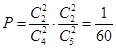 ;(2)通过对立事件发生的概率为
;(2)通过对立事件发生的概率为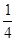 来求,其对立事件包含“取到的4个球只有1个红球”和“取到的4个球全是白球”,从而有
来求,其对立事件包含“取到的4个球只有1个红球”和“取到的4个球全是白球”,从而有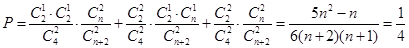 ,化简得7n2-11n-6=0,解得n=2,或
,化简得7n2-11n-6=0,解得n=2,或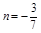 (舍去),故n=2.
(舍去),故n=2.
试题解析:(1)记“取到的4个球全是红球”为事件A,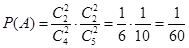 .
.
(2)记“取到的4个球至多有1个红球”为事件B,“取到的4个球只有1个红球”为事件B1,“取到的4个球全是白球”为事件B2,由题意,得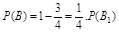

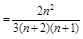

所以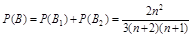
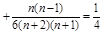 ,
,
化简,得7n2-11n-6=0,解得n=2,或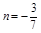 (舍去),故n=2.
(舍去),故n=2.
考点:排列组合与概率计算

练习册系列答案
相关题目
为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
 .(12分)
.(12分)(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为
 ,求
,求 的分布列与期望.
的分布列与期望.下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05[ | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:
 ,其中
,其中 )
)
 ~
~ ,且
,且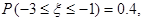 则
则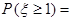 .
.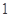 的球
的球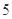 个,编号为
个,编号为 的球
的球 个,这些球的大小完全一样。
个,这些球的大小完全一样。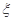 为这三个球的编号之和,求随机变量
为这三个球的编号之和,求随机变量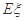 .
.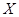 为取出2球中白球的个数,已知
为取出2球中白球的个数,已知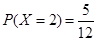 .
. (已知甲回答每道题的正确率相同,并且相互之间没有影响).
(已知甲回答每道题的正确率相同,并且相互之间没有影响).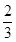 ,则
,则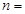 __________
__________ 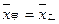 ,方差
,方差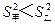 ,则成绩较稳定的同学是 (填“甲”或“乙”)
,则成绩较稳定的同学是 (填“甲”或“乙”)