题目内容
P为四面体S-ABC的侧面SBC内的一点，且侧面SBC垂直于底面ABC，若动点P到底面ABC的距离与到点S的距离相等，则动点P的轨迹是侧面SBC内的（ ）
| A．线段或圆的一部分 | B．椭圆的一部分 |
| C．双曲线的一部分 | D．抛物线的一部分 |
D
解：∵四棱锥S-ABCD∴面SBC不垂直面ABC，过P作PD⊥面ABC于D，过D作DH⊥BC于H，连接PH，
可得BC⊥面DPH，所以BC⊥PH，故∠PHD为二面角S-BC-A的平面角令其为θ
则Rt△PGH中，|PD|：|PH|=sinθ（θ为S-BC-A的二面角）．
又点P到平面ABC距离与到点S的距离相等，即|PS|=|PD|
∴|PS|：|PH|=sinθ≤1，即在平面SBC中，点P到定点S的距离与定直线BC的距离之比是一个常数sinθ，
面SBC不垂直面ABC，所以θ是锐角，故常数sinθ≤1
故由椭圆定义知P点轨迹为椭圆在面SBC内的一部分．
故选D．
练习册系列答案
相关题目
(
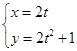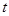为参数)，则过曲线C上横坐标为1的点的切线方程为 .
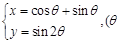为参数
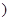化为普通方程．
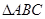,周长为14，
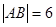,求顶点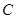
的轨迹方程.
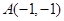．若曲线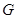
上存在两点
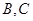，使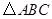
为正三角形，则称
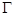型曲线．给定下列三条曲线：
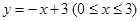； ② 
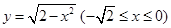； ③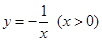 
．
（
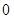
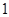
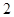
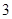
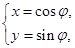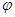为参数）曲线C2的参数方程为
（
，
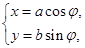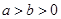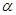与C1，C2各有一个交点.当
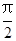时，这两个交点重合.
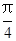时，l与C1，C2的交点分别为A1，B1,当
（
为参数），求椭圆上一点P到直线
（
为参数）的最短距离。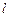
的参数方程是
（
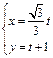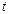是参数），曲线C的极坐标方程是
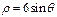，则