题目内容
设数列
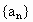 的前n项和为
的前n项和为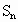 ,若对于任意的n∈N*,都有
,若对于任意的n∈N*,都有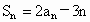 ,
,
(1)
求数列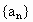 的首项与递推关系式
的首项与递推关系式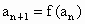 ;
;
(2)
先阅读下面定理,若数列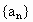 有递推关系:
有递推关系: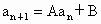 ,其中A、B为常数,且A≠1,B≠0,则数列
,其中A、B为常数,且A≠1,B≠0,则数列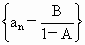 是以A为公比的等比数列,请你在第(1)题的基础上应用本定理,求数列
是以A为公比的等比数列,请你在第(1)题的基础上应用本定理,求数列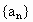 的通项公式;
的通项公式;
(3)
求数列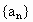 的前n项和
的前n项和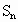 .
.
答案:略
解析:
提示:
解析:
|
(1) 令n=1,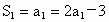 ,∴ ,∴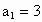 . .
又 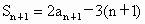 , ,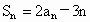 . .
两式相减得 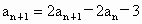 , ,
∴ 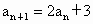 . .
(2) 按照定理A=2,B=3,则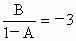 , ,
∴ 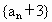 是公比为2的等比数列,其首项为 是公比为2的等比数列,其首项为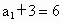 , ,
∴ 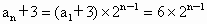 , ,
∴ 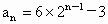 . .
(3)
|
提示:
|
(1) 要建立(2) 给出了一个定理,需同学们自己阅读,考查了观察问题、研究问题的能力.(3) 可用拆项法求和. |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
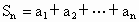
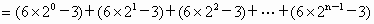
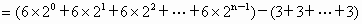
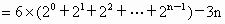
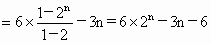
 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,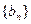 为等比数列,且
为等比数列,且 (Ⅰ)求数列
(Ⅰ)求数列 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.