题目内容
(本小题满分12分)
设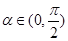 ,函数
,函数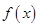 的定义域为
的定义域为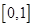 且
且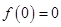 ,
,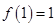 当
当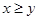 时有
时有

(1)求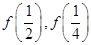 ;
;
(2)求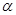 的值;
的值;
(3)求函数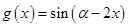 的单调区间.
的单调区间.
设
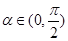 ,函数
,函数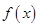 的定义域为
的定义域为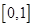 且
且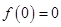 ,
,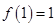 当
当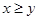 时有
时有
(1)求
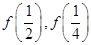 ;
;(2)求
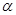 的值;
的值;(3)求函数
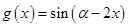 的单调区间.
的单调区间.解:(1)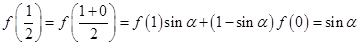 ;
;
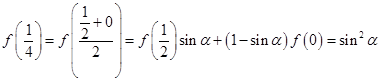
(2)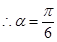 .
.
(3)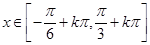
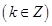 时,
时,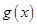 单调递减,
单调递减,
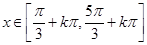
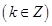 时,
时,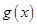 单调递增.
单调递增.
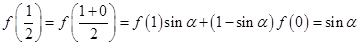 ;
;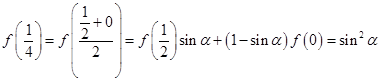
(2)
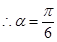 .
.(3)
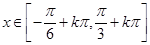
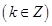 时,
时,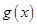 单调递减,
单调递减,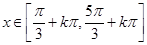
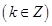 时,
时,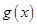 单调递增.
单调递增.本试题主要是考查了三角函数的图像与性质的综合运用,以及函数的递推关系的运用,结合了数列的思想求解特殊的函数值,然后利用三角函数性质得到单调区间。
(1)根据已知条件的,得到函数关系式,赋值可知。
(2)按照上述的规律依次得到函数值的关系式,然后分析求解角的值。
(3)利用三角函数的性质可知,所求解的三角函数的区间与正弦区间的对应关系得到。
解:(1)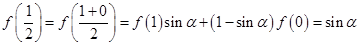 ;
;
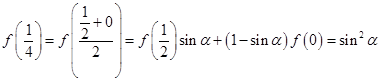
(2)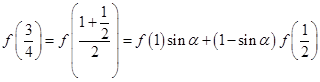

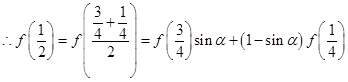

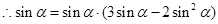
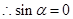 或
或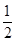 或1
或1
又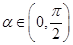 ,
,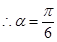 .
.
(3)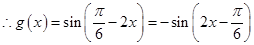
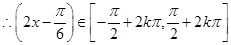 时,
时,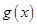 单调递减,
单调递减,
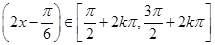 时,
时,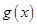 单调递增;
单调递增;
解得:
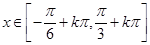
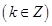 时,
时,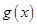 单调递减,
单调递减,
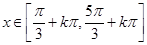
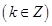 时,
时,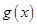 单调递增.
单调递增.
(1)根据已知条件的,得到函数关系式,赋值可知。
(2)按照上述的规律依次得到函数值的关系式,然后分析求解角的值。
(3)利用三角函数的性质可知,所求解的三角函数的区间与正弦区间的对应关系得到。
解:(1)
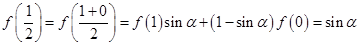 ;
;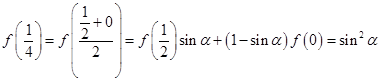
(2)
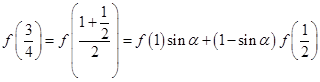

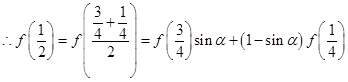

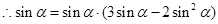
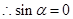 或
或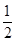 或1
或1又
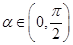 ,
,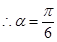 .
.(3)
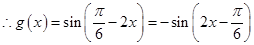
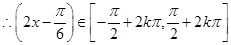 时,
时,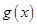 单调递减,
单调递减,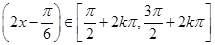 时,
时,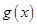 单调递增;
单调递增;解得:
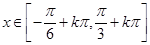
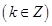 时,
时,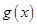 单调递减,
单调递减,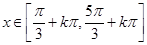
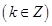 时,
时,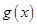 单调递增.
单调递增.
练习册系列答案
相关题目
 的图象向左平移
的图象向左平移 个单位,所得图象的函数解析式为 ( )
个单位,所得图象的函数解析式为 ( )
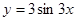


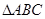 的内角
的内角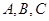 对边的边长分别是
对边的边长分别是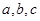 ,
,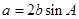 .
.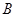 的大小;
的大小;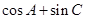 的取值范围.
的取值范围. 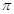 且在
且在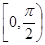 单调递增的是
单调递增的是



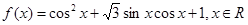 .
.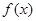 的最小正周期及单调增区间;
的最小正周期及单调增区间;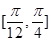 上的最大值和最小值,并求函数取得最大值和最小值时的自变量
上的最大值和最小值,并求函数取得最大值和最小值时的自变量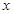 的值.
的值. 的图像可由
的图像可由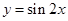 的图像( )
的图像( ) 个单位长度
个单位长度 个单位长度
个单位长度 中,如果满足
中,如果满足 ,则
,则 的取值范围是 .
的取值范围是 . 的图像如图所示,则
的图像如图所示,则
