题目内容
(本小题满分12分)
设锐角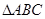 的内角
的内角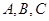 对边的边长分别是
对边的边长分别是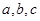 ,
,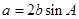 .
.
(1)求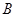 的大小;
的大小;
(2)求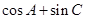 的取值范围.
的取值范围.
设锐角
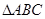 的内角
的内角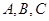 对边的边长分别是
对边的边长分别是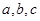 ,
,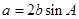 .
.(1)求
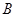 的大小;
的大小;(2)求
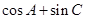 的取值范围.
的取值范围. (1)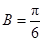 . (2)
. (2)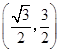 .
.
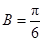 . (2)
. (2)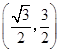 .
.本试题主要考查了三角函数的恒等变换以及解三角形中正弦定理的运用。
(1)利用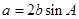 ,化边为角的,得到关于角A的三角方程,求解得到角
,化边为角的,得到关于角A的三角方程,求解得到角
(2)将所求的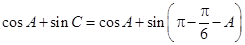 化为一个角的三角函数,借助于三角函数的值域求解得到。
化为一个角的三角函数,借助于三角函数的值域求解得到。
解:(1)由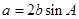 ,根据正弦定理得
,根据正弦定理得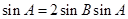 , …………2分
, …………2分
所以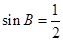 …………3分
…………3分
由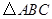 为锐角三角形得
为锐角三角形得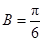 . …………4分
. …………4分
(2)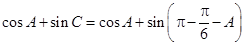
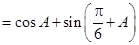
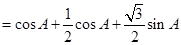
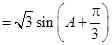 . …………8分
. …………8分
由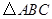 为锐角三角形知,
为锐角三角形知,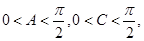 ,得
,得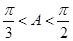 , 所以
, 所以
所以 .
.
由此有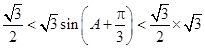 ,
,
所以,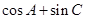 的取值范围为
的取值范围为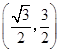 . …………12分
. …………12分
(1)利用
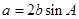 ,化边为角的,得到关于角A的三角方程,求解得到角
,化边为角的,得到关于角A的三角方程,求解得到角(2)将所求的
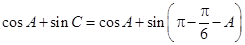 化为一个角的三角函数,借助于三角函数的值域求解得到。
化为一个角的三角函数,借助于三角函数的值域求解得到。解:(1)由
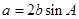 ,根据正弦定理得
,根据正弦定理得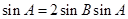 , …………2分
, …………2分所以
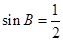 …………3分
…………3分由
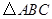 为锐角三角形得
为锐角三角形得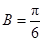 . …………4分
. …………4分(2)
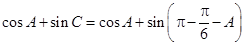
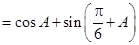
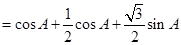
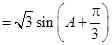 . …………8分
. …………8分由
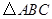 为锐角三角形知,
为锐角三角形知,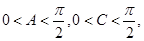 ,得
,得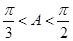 , 所以
, 所以
所以
 .
.由此有
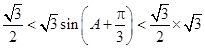 ,
, 所以,
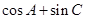 的取值范围为
的取值范围为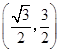 . …………12分
. …………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;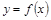 的图像经过怎样的变换才能得到函数
的图像经过怎样的变换才能得到函数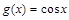 的图像?
的图像?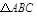 中,
中,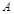 、
、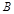 、
、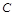 分别为三边
分别为三边 、
、 、
、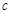 所对的角,若
所对的角,若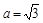 ,
,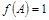 ,求
,求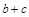 的最大值.
的最大值.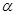 的顶点在原点,始边与
的顶点在原点,始边与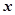 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点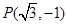 .
. 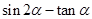 的值;
的值; ,求函数
,求函数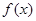 在
在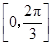 上的单调递增区间.
上的单调递增区间.  (A>0, 0<ω<π)的图象如图所示,则函数的解析式是( )
(A>0, 0<ω<π)的图象如图所示,则函数的解析式是( )
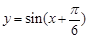



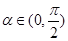 ,函数
,函数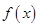 的定义域为
的定义域为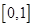 且
且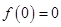 ,
,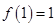 当
当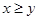 时有
时有
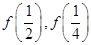 ;
;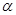 的值;
的值;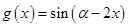 的单调区间.
的单调区间. .
.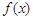 的最小正周期;
的最小正周期; ,求
,求 的值.
的值.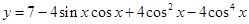 的最大值与最小值.
的最大值与最小值.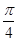 )的图像的一条对称轴是
)的图像的一条对称轴是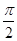
 的值为 .
的值为 .