题目内容
(2012•黄冈模拟)已知坐标平面内定点和动点A(-1,0),B(1,0),M(4,0),N(0,4)和动点P(x1,y1),Q(x2,y2),若
•
=3,
=(
-t)
+(
+t)
,其中O为坐标原点,则|
|的最小值是
| AP |
| BP |
| OQ |
| 1 |
| 2 |
| OM |
| 1 |
| 2 |
| ON |
| PQ |
2
-2
| 2 |
2
-2
.| 2 |
分析:利用向量知识,确定P、Q的轨迹方程,进而利用点到直线的距离公式,即可求|
|的最小值.
| PQ |
解答:解:∵动点A(-1,0),B(1,0),P(x1,y1),
∴
•
=3
∴(x1+1,y1)•(x1-1,y1)=3
∴x12+y12=4
∴P的轨迹是个半径为2、圆心在原点的圆
∵
=(
-t)
+(
+t)
∴Q,M,N三点共线
∵M(4,0),N(0,4)
∴Q的轨迹方程为直线MN:x+y-4=0
∴|
|的最小值是圆心到直线的距离减去半径,即
-2=2
-2
故答案为:2
-2
∴
| AP |
| BP |
∴(x1+1,y1)•(x1-1,y1)=3
∴x12+y12=4
∴P的轨迹是个半径为2、圆心在原点的圆
∵
| OQ |
| 1 |
| 2 |
| OM |
| 1 |
| 2 |
| ON |
∴Q,M,N三点共线
∵M(4,0),N(0,4)
∴Q的轨迹方程为直线MN:x+y-4=0
∴|
| PQ |
| 4 | ||
|
| 2 |
故答案为:2
| 2 |
点评:本题考查轨迹方程,考查向量知识的运用,确定P、Q的轨迹方程是关键.

练习册系列答案
相关题目
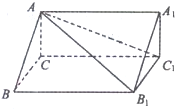 (2012•黄冈模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=
(2012•黄冈模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=