题目内容
【题目】已知数列{an}，{bn}满足 
， 
，其中n∈N+ ． （I）求证：数列{bn}是等差数列，并求出数列{an}的通项公式；
（II）设 
，求数列{cncn+2}的前n项和为Tn ．
【答案】（Ⅰ）证明：∵ 
= 
= 
，
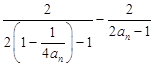∴数列{bn}是公差为2的等差数列，
又 
，∴bn=2+（n﹣1）×2=2n，
∴ 
，解得 
． …
（Ⅱ）解：由（Ⅰ）可得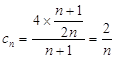 
，
∴ 
，
∴数列{cncn+2}的前n项和为
= 
．
【解析】（I）作差利用递推关系、等差数列的通项公式即可得出．（II）利用“裂项求和”方法即可得出．
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系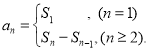
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
练习册系列答案
教材全解字词句篇系列答案
相关题目
【题目】乡大学生携手回乡创业，他们引进某种果树在家乡进行种植试验．他们分别在五种不同的试验田中种植了这种果树100株并记录了五种不同的试验田中果树的死亡数，得到如下数据：
试验田 | 试验田1 | 试验田2 | 试验田3 | 试验田4 | 试验田5 |
死亡数 | 23 | 32 | 24 | 29 | 17 |
（Ⅰ）求这五种不同的试验田中果树的平均死亡数；
（Ⅱ）从五种不同的试验田中随机取两种试验田的果树死亡数，记为x，y，用（x，y）的形式列出所有的基本事件，其中（x，y）和（y，x）视为同一事件，并求
的概率．
