题目内容
11．证明函数f（x）=$\frac{2-x}{x+2}$在（-2，+∞）上是增函数．分析 根据函数单调性的定义证明即可．
解答 解：f（x）=$\frac{2-x}{x+2}$=-1+$\frac{4}{x+2}$，
设x1＞x2＞-2，
则f（x1）-f（x2）
=$\frac{4}{{x}_{1}+2}$-$\frac{4}{{x}_{2}+2}$
=$\frac{4{（x}_{2}{-x}_{1}）}{{（x}_{1}+2）{（x}_{2}+2）}$，
∵x2＜x1，
∴f（x1）-f（x2）＜0，
∴f（x）在（-2，+∞）递减．
点评 本题解出了函数的单调性的证明，是一道基础题．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
2．与向量$\overrightarrow d=（12，5）$平行的单位向量为（ ）
| A． | $（\frac{12}{13}，5）$ | B． | $（-\frac{12}{13}，-\frac{5}{13}）$ | ||
| C． | $（\frac{12}{13}，\frac{5}{13}）$或$（-\frac{12}{13}，-\frac{5}{13}）$ | D． | $（±\frac{12}{13}，±\frac{5}{13}）$ |
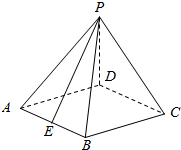如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠DAB=60°，平面PED⊥平面PAB，PD⊥AD，点E为AB中点．
（1）求证：BC⊥SB；