题目内容
设F1(-1,0),F2(1,0),动点M满足|MF1|+|MF2|=2
.
(1)求M的轨迹C的方程;
(2)设直线l:y=
(x-1)与曲线C交于A、B两点,求
•
的值.
| 2 |
(1)求M的轨迹C的方程;
(2)设直线l:y=
| ||
| 7 |
| F1A |
| F1B |
分析:(1)直接由椭圆的定义得到所求动点M的轨迹为椭圆,由已知条件求出a和c,继而求出b的值,则轨迹方程可求;
(2)联立直线和椭圆方程,化为关于x的一元二次方程,设出交点坐标,由根与系数关系得到两交点的横纵坐标的和与积,写出向量的坐标表示,展开数量积运算,代入根与系数关系后整理得答案.
(2)联立直线和椭圆方程,化为关于x的一元二次方程,设出交点坐标,由根与系数关系得到两交点的横纵坐标的和与积,写出向量的坐标表示,展开数量积运算,代入根与系数关系后整理得答案.
解答:解:(1)设动点M(x,y),
∵F1(-1,0),F2(1,0),∴|MF1|+|MF2|=2
>2=|F1F2|,
则M的轨迹为以F1,F2为焦点,以2
为长轴的椭圆,
则a=
,c=1,b2=a2-c2=1.
方程为:
+y2=1;
(2)联立
,得9x2-4x-12=0.
设A(x1,y1),B(x2,y2),
则x1+x2=
,x1x2=-
.
=(x1+1,y1),
=(x2+1,y2),
∴
•
=(x1+1,y1)•(x2+1,y2)
=(x1+1)(x2+1)+y1y2=
x1x2+
(x1+x2)+
=
×(-
)+
×
+
=0.
∵F1(-1,0),F2(1,0),∴|MF1|+|MF2|=2
| 2 |
则M的轨迹为以F1,F2为焦点,以2
| 2 |
则a=
| 2 |
方程为:
| x2 |
| 2 |
(2)联立
|
设A(x1,y1),B(x2,y2),
则x1+x2=
| 4 |
| 9 |
| 12 |
| 9 |
| F1A |
| F1B |
∴
| F1A |
| F1B |
=(x1+1)(x2+1)+y1y2=
| 8 |
| 7 |
| 6 |
| 7 |
| 8 |
| 7 |
=
| 8 |
| 7 |
| 12 |
| 9 |
| 6 |
| 7 |
| 4 |
| 9 |
| 8 |
| 7 |
点评:本题考查了轨迹方程的求法,考查了平面向量的数量积运算,训练了“设而不求”的解题思想方法,是中档题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目

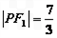 ,求曲线E的标准方程;
,求曲线E的标准方程;