题目内容
设动点P到两定点F1(-1,0 )和F2(1,0 ) 的距离分别为d1和d2,∠F1PF2=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ,
(1)证明:动点P的轨迹C为双曲线,并求出C的方程;
(2)如图过点F2的直线与双曲线C的右支交于A、B两点,问:是否存在λ,使△F1AB是以点B为直角顶点的等腰直角三角形?若存在,求出λ的值;若不存在,说明理由。
(1)证明:动点P的轨迹C为双曲线,并求出C的方程;
(2)如图过点F2的直线与双曲线C的右支交于A、B两点,问:是否存在λ,使△F1AB是以点B为直角顶点的等腰直角三角形?若存在,求出λ的值;若不存在,说明理由。

解:(1)在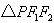 中,
中,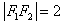 ,
,
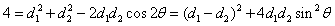 ,
,
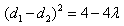 ,
,
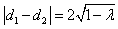 (小于2的常数),
(小于2的常数),
故动点P的轨迹C是以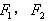 为焦点,实轴长
为焦点,实轴长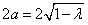 的双曲线,
的双曲线,
方程为 。
。
(2)在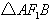 中,设
中,设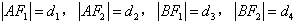 ,
,
假设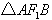 为等腰直角三角形,则
为等腰直角三角形,则
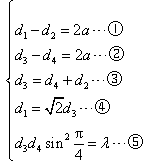
由②与③得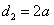 ,
,
则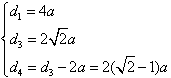 ,
,
由⑤得 ,
,
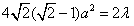 ,
,
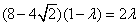 ,
,
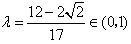 ,
,
故存在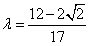 满足题设条件。
满足题设条件。
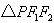 中,
中,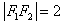 ,
,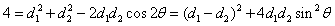 ,
,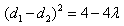 ,
,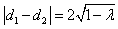 (小于2的常数),
(小于2的常数),故动点P的轨迹C是以
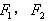 为焦点,实轴长
为焦点,实轴长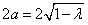 的双曲线,
的双曲线,方程为
 。
。(2)在
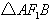 中,设
中,设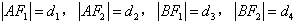 ,
,假设
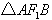 为等腰直角三角形,则
为等腰直角三角形,则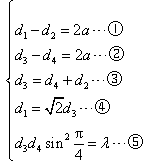
由②与③得
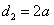 ,
,则
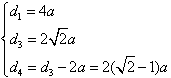 ,
,由⑤得
 ,
,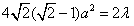 ,
,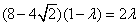 ,
,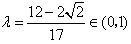 ,
,故存在
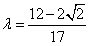 满足题设条件。
满足题设条件。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 设动点P到两定点F1(-l,0)和F2(1,0)的距离分别为d1和d2,∠F1PF2=2θ,且存在常数λ(0<λ<1),使得d1d2 sin2θ=λ.
设动点P到两定点F1(-l,0)和F2(1,0)的距离分别为d1和d2,∠F1PF2=2θ,且存在常数λ(0<λ<1),使得d1d2 sin2θ=λ.