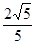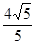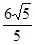题目内容
已知曲线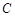 上动点
上动点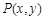 到定点
到定点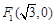 与定直线
与定直线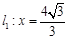 的距离之比为常数
的距离之比为常数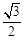 .
.
(1)求曲线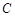 的轨迹方程;
的轨迹方程;
(2)若过点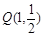 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点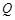 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;
(3)以曲线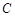 的左顶点
的左顶点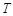 为圆心作圆
为圆心作圆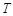 :
: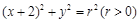 ,设圆
,设圆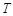 与曲线
与曲线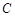 交于点
交于点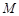 与点
与点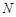 ,求
,求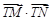 的最小值,并求此时圆
的最小值,并求此时圆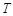 的方程.
的方程.
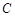 上动点
上动点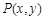 到定点
到定点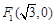 与定直线
与定直线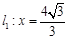 的距离之比为常数
的距离之比为常数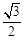 .
.(1)求曲线
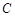 的轨迹方程;
的轨迹方程;(2)若过点
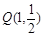 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点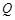 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;(3)以曲线
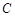 的左顶点
的左顶点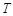 为圆心作圆
为圆心作圆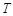 :
: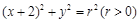 ,设圆
,设圆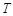 与曲线
与曲线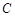 交于点
交于点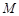 与点
与点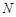 ,求
,求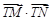 的最小值,并求此时圆
的最小值,并求此时圆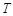 的方程.
的方程.(1)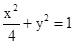 (2)
(2)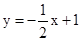 (3)
(3)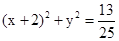
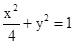 (2)
(2)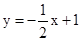 (3)
(3)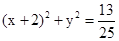
第一问利用(1)过点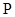 作直线
作直线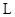 的垂线,垂足为D.
的垂线,垂足为D.
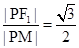 代入坐标得到
代入坐标得到
第二问当斜率k不存在时,检验得不符合要求;
当直线l的斜率为k时, ;,化简得
;,化简得
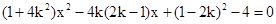
第三问点N与点M关于X轴对称,设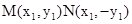 ,, 不妨设
,, 不妨设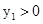 .
.
由于点M在椭圆C上,所以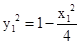 .
.
由已知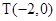 ,则
,则
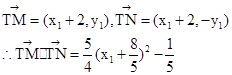 ,
,
由于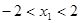 ,故当
,故当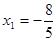 时,
时,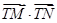 取得最小值为
取得最小值为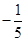 .
.
计算得,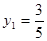 ,故
,故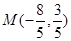 ,又点
,又点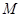 在圆
在圆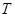 上,代入圆的方程得到
上,代入圆的方程得到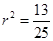 .
.
故圆T的方程为: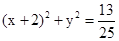
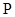 作直线
作直线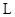 的垂线,垂足为D.
的垂线,垂足为D.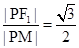 代入坐标得到
代入坐标得到第二问当斜率k不存在时,检验得不符合要求;
当直线l的斜率为k时,
 ;,化简得
;,化简得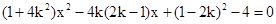
第三问点N与点M关于X轴对称,设
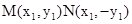 ,, 不妨设
,, 不妨设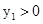 .
.由于点M在椭圆C上,所以
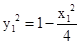 .
. 由已知
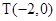 ,则
,则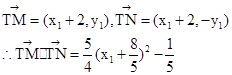 ,
,由于
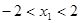 ,故当
,故当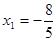 时,
时,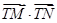 取得最小值为
取得最小值为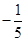 .
.计算得,
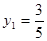 ,故
,故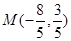 ,又点
,又点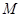 在圆
在圆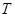 上,代入圆的方程得到
上,代入圆的方程得到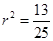 .
. 故圆T的方程为:
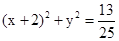

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,动点
,动点 满足
满足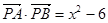 ,则动点
,则动点 的轨迹是 。
的轨迹是 。 在点P处的切线
在点P处的切线 分别交x轴、y轴于不同的两点A、B,
分别交x轴、y轴于不同的两点A、B, 。当点P在C上移动时,点M的轨迹为D。
。当点P在C上移动时,点M的轨迹为D。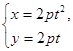 (t为参数),其中p>0,焦点为F,准线为
(t为参数),其中p>0,焦点为F,准线为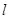 . 过抛物线上一点M作
. 过抛物线上一点M作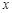 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为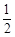 ,且经过点
,且经过点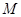
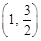 .
.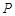 (2,1)的直线
(2,1)的直线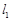 与椭圆
与椭圆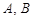 ,满足
,满足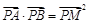 ?若存在,求出直线
?若存在,求出直线 ,讨论方程
,讨论方程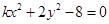 所表示的圆锥曲线类型,并求其焦点坐标
所表示的圆锥曲线类型,并求其焦点坐标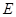 :
: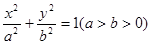 的左焦点
的左焦点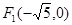 ,若椭圆上存在一点
,若椭圆上存在一点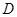 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段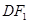 相切于线段
相切于线段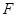 .
.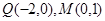 及椭圆
及椭圆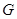 :
: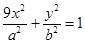 ,过点
,过点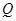 作斜率为
作斜率为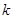 的直线
的直线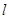 交椭圆
交椭圆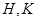 两点,设线段
两点,设线段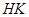 的中点为
的中点为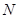 ,连结
,连结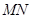 ,试问当
,试问当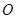 的直线交椭圆
的直线交椭圆 :
: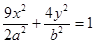 于
于 、
、 两点,其中
两点,其中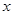 轴的垂线,垂足为
轴的垂线,垂足为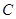 ,连结
,连结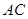 并延长交椭圆
并延长交椭圆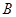 ,求证:
,求证: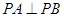
 的准线方程是
的准线方程是
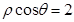


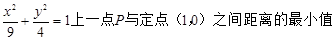 ( )。
( )。