题目内容
已知函数f（x）=ax3+
-3 （x≠0）（a、b为常数），若f（3）=2，则f（-3）=________．
-8
分析：先利用f（3）=2求出a×33+
=5，再对f（-3）进行整理变形把所求整体代入即可求出f（-3）的值．
解答：因为f（3）=a×33+-3=2?a×33+=5，
所以f（-3）=a×（-3）3+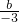
-3=-（a×33+）-3=-5-3=-8．
故答案为：-8．
点评：本题考查函数的奇偶性以及整体代入的思想．是对基础知识的考查，属于基础题．
分析：先利用f（3）=2求出a×33+
=5，再对f（-3）进行整理变形把所求整体代入即可求出f（-3）的值．解答：因为f（3）=a×33+
-3=2?a×33+=5，所以f（-3）=a×（-3）3+
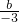-3=-（a×33+）-3=-5-3=-8．故答案为：-8．
点评：本题考查函数的奇偶性以及整体代入的思想．是对基础知识的考查，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目