题目内容
已知△ABC中,下列条件解三角形,其中有唯一解的个数为( )
①A=60°,a=
,b=1;
②A=30°,a=1,b=2;
③A=30°,a=6,c=10;
④A=45°,a=2,b=2
.
①A=60°,a=
| 3 |
②A=30°,a=1,b=2;
③A=30°,a=6,c=10;
④A=45°,a=2,b=2
| 6 |
分析:根据已知条件利用正弦定理求得sinB的值,再根据大边对大角确定B的个数,从而确定三角形的解的个数.
解答:解:已知△ABC中,对于①A=60°,a=
,b=1,根据正弦定理以及大边对大角,可得角B唯一,故三角形有唯一解.
对于②A=30°,a=1,b=2,由正弦定理可得
=
,∴sinB=
,再由大边对大角可得B=150°,故三角形
有唯一解.
对于③A=30°,a=6,c=10,由正弦定理可得
=
,解得sinC=
,∵C>A,∴C值有2个,一个为锐角,
另一个为钝角,故三角形有2个解.
对于④A=45°,a=2,b=2
,由正弦定理可得
=
,解得sinB=
,故B不存在,故三角形无解.
故选C.
| 3 |
对于②A=30°,a=1,b=2,由正弦定理可得
| 1 |
| sin30° |
| 2 |
| sinB |
| 1 |
| 2 |
有唯一解.
对于③A=30°,a=6,c=10,由正弦定理可得
| 10 |
| sinC |
| 6 |
| sin30° |
| 5 |
| 6 |
另一个为钝角,故三角形有2个解.
对于④A=45°,a=2,b=2
| 6 |
| 2 |
| sin45° |
2
| ||
| sinB |
| 3 |
故选C.
点评:本题主要考查利用正弦定理以及大边对大角解三角形,根据三角函数的值求角,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,b=1;
,b=1;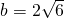 .
.