题目内容
12.求函数f(x)=$\frac{4}{2-{x}^{2}}$的图形的渐近线.分析 分两类求解:①水平渐近线,②垂直渐近线,都是通过取极限的方式确定其方程.
解答 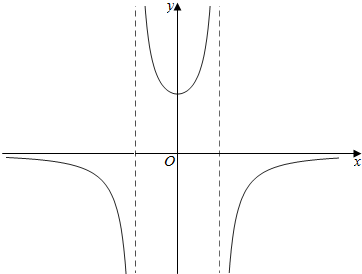 解:函数f(x)图象的渐近线有两类:
解:函数f(x)图象的渐近线有两类:
①水平渐近线,
$\underset{lim}{x→+∞}$f(x)=$\underset{lim}{x→+∞}$$\frac{4}{2-{x}^{2}}$=0,
$\underset{lim}{x→-∞}$f(x)=$\underset{lim}{x→+∞}$$\frac{4}{2-{x}^{2}}$=0,
由此可知,y=0为该函数图象的渐近线;
②垂直渐近线,
令2-x2=0解得,x=$\sqrt{2}$或x=-$\sqrt{2}$,
即$\underset{lim}{x→\sqrt{2}}$f(x)=∞,$\underset{lim}{x→-\sqrt{2}}$f(x)=∞,
综合得,该函数有三条渐近线,方程分别为:
y=0,x=-$\sqrt{2}$,x=$\sqrt{2}$(如右图).
点评 本题主要考查了函数的图象和性质,涉及函数图象的渐近线的求法,属于基础题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
7.某大学餐饮中心为了解新生的饮食习惯,在全校-年级学生中进行随机抽职了100名学生进行调查.调查结果如表所示:
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)将上述调查所得到学生喜欢甜品的频率视为概率.现在从该大学一年级学生中,采用随机抽样的方法抽职1名学生,抽职5次,记被抽取的5名学生中的“喜欢甜品人数”为X.若每次抽职结果是相互独立的,求期望E(X)和方差D(X).
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(c+d)(b+d)}$,
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | 60 | 10 | 70 |
| 北方学生 | 20 | 10 | 30 |
| 合计 | 80 | 20 | 100 |
(2)将上述调查所得到学生喜欢甜品的频率视为概率.现在从该大学一年级学生中,采用随机抽样的方法抽职1名学生,抽职5次,记被抽取的5名学生中的“喜欢甜品人数”为X.若每次抽职结果是相互独立的,求期望E(X)和方差D(X).
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(c+d)(b+d)}$,
| P(K2≥K) | 0.100 | 0.050 | 0.010 |
| K | 2.706 | 3.841 | 6.635 |
4.平行于x轴,且过点(3,2)的直线的方程为( )
| A. | x=3 | B. | y=2 | C. | y=$\frac{3}{2}$x | D. | y=$\frac{2}{3}$x |