题目内容
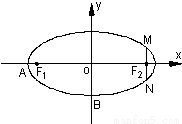
已知椭圆E的左,右焦点坐标分别为(-2,0),(2,0),离心率是
,过左焦点任作一条与坐标轴不垂直的直线交E于A、B两点.
(1)求E的方程;
(2)已知点M(-3,0),试判断直线AM与直线BM的倾斜角是否总是互补,并说明理由.
| ||
| 3 |
(1)求E的方程;
(2)已知点M(-3,0),试判断直线AM与直线BM的倾斜角是否总是互补,并说明理由.
分析:(1)设椭圆方程为
+
=1(a>b>0),由题意知
,由此能求出椭圆方程.
(2)直线AM与直线BM的倾斜角总是互补.理由如下:设AB的方程为:y=k(x+2),k≠0,联立
,得(1+3k2)x2+12k2x+12k2-6=0,设A(x1,y1),B(x2,y2),x1+x2=
,x1•x2=
,由此得到kAM=-kBM,故直线AM与直线BM的倾斜角总是互补.
| x2 |
| a2 |
| y2 |
| b2 |
|
(2)直线AM与直线BM的倾斜角总是互补.理由如下:设AB的方程为:y=k(x+2),k≠0,联立
|
| -12k2 |
| 1+3k2 |
| 12k2-6 |
| 1+3k2 |
解答:解:(1)设椭圆方程为
+
=1(a>b>0),
由题意知
,
解得a2=6,b2=2,
∴椭圆方程为
+
=1.
(2)直线AM与直线BM的倾斜角总是互补.理由如下:
根据题意设AB的方程为:y=k(x+2),k≠0,
联立
,得(1+3k2)x2+12k2x+12k2-6=0,
设A(x1,y1),B(x2,y2),
x1+x2=
,①
x1•x2=
,②
kAM+kBM=
+
=
+
=
,
把①②代入,得2x1x2+5(x1+x2)+12=0,
∴kAM+kBM=0,即kAM=-kBM,
∴直线AM与直线BM的倾斜角总是互补.
| x2 |
| a2 |
| y2 |
| b2 |
由题意知
|
解得a2=6,b2=2,
∴椭圆方程为
| x2 |
| 6 |
| y2 |
| 2 |
(2)直线AM与直线BM的倾斜角总是互补.理由如下:
根据题意设AB的方程为:y=k(x+2),k≠0,
联立
|
设A(x1,y1),B(x2,y2),
x1+x2=
| -12k2 |
| 1+3k2 |
x1•x2=
| 12k2-6 |
| 1+3k2 |
kAM+kBM=
| y1 |
| x1+3 |
| y2 |
| x2+3 |
=
| k(x1+2) |
| x1+3 |
| k(x2+2) |
| x2+3 |
=
| k[2x1x2+5(x1+x2)+12] |
| x1x2+3(x1+x2)+9 |
把①②代入,得2x1x2+5(x1+x2)+12=0,
∴kAM+kBM=0,即kAM=-kBM,
∴直线AM与直线BM的倾斜角总是互补.
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,椭圆方程的求法.考查运算求解能力,推理论证能力;考查化归与转化思想.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
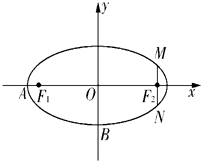 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:
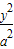 +
+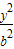 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=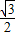 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的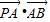 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
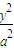 +
+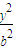 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=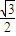 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的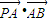 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.