Question

【题目】已知二次函数f（x）=mx2﹣2x﹣3，关于实数x的不等式f（x）≤0的解集为（﹣1，n）
（1）当a＞0时，解关于x的不等式：ax2+n+1＞（m+1）x+2ax；
（2）是否存在实数a∈（0，1），使得关于x的函数y=f（ax）﹣3ax+1（x∈[1，2]）的最小值为﹣5？若存在，求实数a的值；若不存在，说明理由．

Answer 1

【答案】
（1）解：由不等式mx2﹣2x﹣3≤0的解集为（﹣1，n）知

关于x的方程mx2﹣2x﹣3=0的两根为﹣1和n，且m＞0

由根与系数关系，得 ∴ ，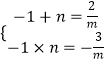

所以原不等式化为（x﹣2）（ax﹣2）＞0，

①当0＜a＜1时，原不等式化为 ，且 ，解得 或x＜2；

②当a=1时，原不等式化为（x﹣2）2＞0，解得x∈R且x≠2；③

④当a＞1时，原不等式化为 ，且 ，解得 或x＞2；

综上所述

当0＜a≤1时，原不等式的解集为 或x＜2}；

当1＜a＜2时，原不等式的解集为{x|x＞2或 ．

（2）解：假设存在满足条件的实数a，

由（1）得：m=1，

∴f（x）=x2﹣2x﹣3，

∴y=f（ax）﹣3ax+1

=a2x﹣2ax﹣3﹣3ax+1

=（ax）2﹣（3a+2）ax﹣3，

令ax=t，（a2≤t≤a），

则y=t2﹣（3a+2）t﹣3

∴对称轴为：t= ，

又0＜a＜1，

∴a2＜a＜1，1＜ ＜ ，

∴函数y=t2﹣（3a+2）t﹣3在[a2，a]递减，

∴t=a时，y最小为：y=﹣2a2﹣2a﹣3=﹣5，

解得：a= ，

【解析】（1）根据韦达定理得方程组求出m，n的值，再通过讨论a的范围，从而求出不等式的解集；（2）把m=1代入方程，得出y=（ax）2﹣（3a+2）ax﹣3，令ax=t，（a2≤t≤a），则y=t2﹣（3a+2）t﹣3，得出函数的单调性，从而表示出y=f（t）的最小值，进而求出a的值．
【考点精析】关于本题考查的二次函数的性质，需要了解当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减才能得出正确答案．