题目内容
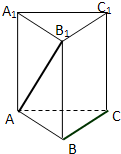 (2011•甘肃模拟)已知正三棱柱ABC-A1B1C1中,底面边长AB=2BB1,则异面直线AB1与BC所成的角的余弦值是( )
(2011•甘肃模拟)已知正三棱柱ABC-A1B1C1中,底面边长AB=2BB1,则异面直线AB1与BC所成的角的余弦值是( )分析:由正三棱柱的性质,可得异面直线AB1与BC所成的角为∠AB1C1或其补角,设B1C1=2,则 BB1 =1,△AB1C1 中,由余弦定理可得cos∠AB1C1=
,从而得到异面直线AB1与BC所成的角的余弦值.
| ||
| 5 |
解答:解:正三棱柱ABC-A1B1C1中,底面边长AB=2BB1,则异面直线AB1与BC所成的角为∠AB1C1或其补角,
△AB1C1 中,设B1C1=2,则 BB1 =1,AC1=
=
=
=AB1,
△AB1C1 中,由余弦定理可得 AC12=AB12+B1C12-2AB1•B1C1cos∠AB1C1,
即 5=5+4-2×
×2cos∠AB1C1,∴cos∠AB1C1=
,
故异面直线AB1与BC所成的角的余弦值是
.
△AB1C1 中,设B1C1=2,则 BB1 =1,AC1=
| AC2+CC12 |
| 4+1 |
| 5 |
△AB1C1 中,由余弦定理可得 AC12=AB12+B1C12-2AB1•B1C1cos∠AB1C1,
即 5=5+4-2×
| 5 |
| ||
| 5 |
故异面直线AB1与BC所成的角的余弦值是
| ||
| 5 |
点评:本题主要考查正三棱柱的性质,异面直线所成的角的定义和求法,余弦定理的应用,属于中档题.

练习册系列答案
相关题目
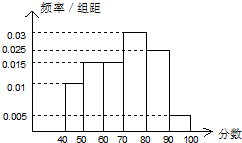 (2011•甘肃模拟)如图所示的是某班60名同学参加2011年高中数学毕业会考所得成绩(成绩均为整数)整理后画出的频率分布直方图,根据图中可得出的该班不及格(60分以下)的同学的人数为
(2011•甘肃模拟)如图所示的是某班60名同学参加2011年高中数学毕业会考所得成绩(成绩均为整数)整理后画出的频率分布直方图,根据图中可得出的该班不及格(60分以下)的同学的人数为