题目内容
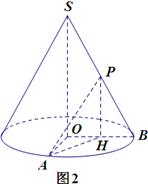
已知圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点且SM=x,从点M拉一绳子,围绕圆锥侧面转到点A.
(1)求绳子的最短长度的平方f(x);
(2)求绳子最短时,定点S到绳子的最短距离;
(3)求f(x)的最大值.
(1)求绳子的最短长度的平方f(x);
(2)求绳子最短时,定点S到绳子的最短距离;
(3)求f(x)的最大值.
分析:(1)算出侧面展开扇形圆心角α=90°,因此将圆锥侧面展开,可得绳子的最短长度为Rt△ASM中斜边AM的长,由此利用勾股定理即可算出f(x)的表达式;
(2)由平面几何性质,可得绳子最短时定点S到绳子的最短距离等于Rt△ASM的斜边上的高,利用三角形面积等积变换求解,可得这个最短距离的表达式;
(3)由于f(x)=x2+16在区间[0,4]上是一个增函数,可得当x=4时,f(x)的最大值等于32.
(2)由平面几何性质,可得绳子最短时定点S到绳子的最短距离等于Rt△ASM的斜边上的高,利用三角形面积等积变换求解,可得这个最短距离的表达式;
(3)由于f(x)=x2+16在区间[0,4]上是一个增函数,可得当x=4时,f(x)的最大值等于32.
解答:解:(1)∵底面半径r=1,母线长l=4,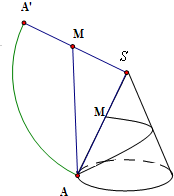
∴侧面展开扇形的圆心角α=
×360°=90°
因此,将圆锥侧面展开成一个扇形,从点M拉一绳子围绕圆锥侧面转到点A,最短距离为Rt△ASM中,斜边AM的长度
∵SM=x,SA=4
∴f(x)=AM2=x2+42=x2+16
(2)由(1)可得:绳子最短时,定点S到绳子的最短距离等于Rt△ASM的斜边上的高,设这个距离等于d,
则d=
=
;
(3)∵f(x)=x2+16,其中0≤x≤4
∴当x=4时,f(x)的最大值等于32.

∴侧面展开扇形的圆心角α=
| r |
| l |
因此,将圆锥侧面展开成一个扇形,从点M拉一绳子围绕圆锥侧面转到点A,最短距离为Rt△ASM中,斜边AM的长度
∵SM=x,SA=4
∴f(x)=AM2=x2+42=x2+16
(2)由(1)可得:绳子最短时,定点S到绳子的最短距离等于Rt△ASM的斜边上的高,设这个距离等于d,
则d=
| SM•AS |
| AM |
| 4x | ||
|
(3)∵f(x)=x2+16,其中0≤x≤4
∴当x=4时,f(x)的最大值等于32.
点评:本题在圆锥的表面拉一根绳子,求绳子长度的最小值.着重考查了圆锥的侧面展开、勾股定理与三角形面积公式等知识,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目

 的侧面积为
的侧面积为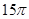 ,底面半径
,底面半径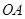 和
和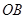 互相垂直,且
互相垂直,且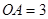 ,
, 是母线
是母线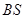 的中点.
的中点.
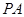 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示). 得
得 ,故
,故
 .2中取OB中点H,联结PH,AH.
.2中取OB中点H,联结PH,AH.  (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角. 平面OAB,
平面OAB, PH
PH OAH中,由OA
OAH中,由OA ;
; 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan