题目内容
在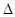 ABC的边AB,BC,CA上分别取D,E,F.使得DE=BE,FE=CE,又点O是△ADF的外心。
ABC的边AB,BC,CA上分别取D,E,F.使得DE=BE,FE=CE,又点O是△ADF的外心。
(Ⅰ)证明:D,E,F,O四点共圆;
(Ⅱ)证明:O在∠DEF的平分线上.
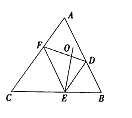
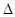 ABC的边AB,BC,CA上分别取D,E,F.使得DE=BE,FE=CE,又点O是△ADF的外心。
ABC的边AB,BC,CA上分别取D,E,F.使得DE=BE,FE=CE,又点O是△ADF的外心。
(Ⅰ)证明:D,E,F,O四点共圆;
(Ⅱ)证明:O在∠DEF的平分线上.
(Ⅰ)由角间的关系可以证明 (Ⅱ)由角相等来证明
试题分析:(Ⅰ) 如图,
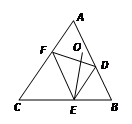
∠DEF=180°-(180°-2∠B)-(180°-2∠C)=180°-2∠A.
因此∠A是锐角,
从而 的外心与顶点A在DF的同侧,
的外心与顶点A在DF的同侧,
∠DOF=2∠A=180°-∠DEF.
因此D,E,F,O四点共圆.
(Ⅱ)由(Ⅰ)知,∠DEO=∠DFO=∠FDO=∠FEO,
即O在∠DEF的平分线上.
点评:本题主要考查了四点共圆,勾股定理,全等三角形的性质和判定,确定圆的条件等知识点,作辅助线构造全等三角形是解此题的关键.
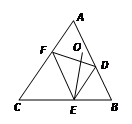
∠DEF=180°-(180°-2∠B)-(180°-2∠C)=180°-2∠A.
因此∠A是锐角,
从而
 的外心与顶点A在DF的同侧,
的外心与顶点A在DF的同侧,∠DOF=2∠A=180°-∠DEF.
因此D,E,F,O四点共圆.
(Ⅱ)由(Ⅰ)知,∠DEO=∠DFO=∠FDO=∠FEO,
即O在∠DEF的平分线上.
点评:本题主要考查了四点共圆,勾股定理,全等三角形的性质和判定,确定圆的条件等知识点,作辅助线构造全等三角形是解此题的关键.

练习册系列答案
相关题目
 的顶点都在半径为3的球的球面上,那么该长方体表面积的最大值等于_____________;
的顶点都在半径为3的球的球面上,那么该长方体表面积的最大值等于_____________;




 ,腰和上底均为1. 如图,则平面图形的实际面积为 。
,腰和上底均为1. 如图,则平面图形的实际面积为 。

 π
π


 cm3(
cm3( cm3
cm3 cm3
cm3 cm3
cm3 的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为

 和
和





