题目内容
(2007•温州一模)某高校在进行自主招生面试时,共设3道试题,每道试题回答正确给10分、否则都不给分.
(Ⅰ)试问某学生参加面试得分为20分的不同情况有几种?
(Ⅱ)若某学生对各道试题回答正确的概率均为
,设他的得分为ξ,试求出ξ的分布列及期望Eξ
(Ⅰ)试问某学生参加面试得分为20分的不同情况有几种?
(Ⅱ)若某学生对各道试题回答正确的概率均为
| 2 | 3 |
分析:(I)根据题意可得:某学生参加面试得分为20的不同情况有C32=3种.
(II)由题意可得:ξ可能取的值为:0,10,20,30,再分布求出其发生的概率,进而求出其分布列与数学期望.
(II)由题意可得:ξ可能取的值为:0,10,20,30,再分布求出其发生的概率,进而求出其分布列与数学期望.
解答:解:(I)根据题意可得:某学生参加面试得分为20,即他答对了两道题,
所以不同情况有C32=3种.---(5分)
(II)由题意可得:ξ可能取的值为:0,10,20,30,
则有P(ξ=0)=
×
×
=
,P(ξ=10)=
×
×(
)2=
,P(ξ=20)=
×(
)2×
=
,P(ξ=30)=
×(
)3=
,
所以ξ分布列如表所示:
所以ξ的数学期望为:Eξ=0×
+10 ×
+20×
+30×
=20.
所以不同情况有C32=3种.---(5分)
(II)由题意可得:ξ可能取的值为:0,10,20,30,
则有P(ξ=0)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| C | 1 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
| C | 3 3 |
| 2 |
| 3 |
| 8 |
| 27 |
所以ξ分布列如表所示:
| ξ | 0 | 10 | 20 | 30 | ||||||||
| P |
|
|
|
|
| 1 |
| 27 |
| 2 |
| 9 |
| 4 |
| 9 |
| 8 |
| 27 |
点评:解决此类问题的关键是熟练掌握离散型随机变量的分布列与数学期望,以及独立重复试验的概率公式,此题属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
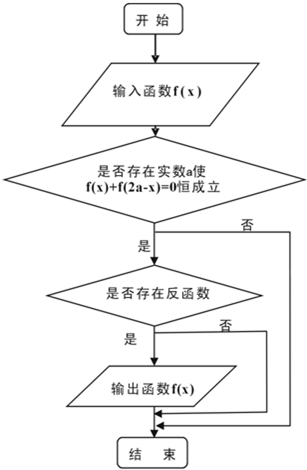 (2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )
(2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )