题目内容
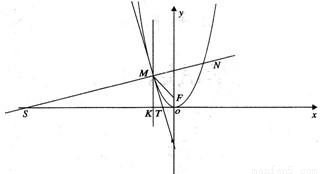
过曲线上一点与以此点为切点的切线垂直的直线，叫做曲线在该点的法线．已知抛物线C的方程为y=ax2（a＞0，x≠0）．点M（x，y）是C上任意点，过点M作C的切线l，法线m．
（I）求法线m与抛物线C的另一个交点N的横坐标xN取值范围；
（II）设点F是抛物线的焦点，连接FM，过点M作平行于y轴的直线n，设m与x轴的交点为S，n与x轴的交点为K，设l与x轴的交点为T，求证∠SMK=∠FMN
【答案】分析：（Ⅰ）将直线m的方程与抛物线C的方程组成方程组，消去y得到关于x的方程，再根据根与系数的关系求得N点的横坐标的表达式，最后根据函数的值域求出其范围即可；
（Ⅱ）欲证∠SMK=∠FMN，即要证∠TMK=∠FMT，为了证角相等，只要证明直线n是∠FMK的平分线，故只要证明T到直线n和直线MF距离相等即可．
解答：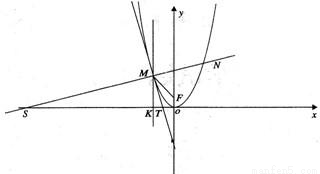
解：（Ⅰ）易得直线m的方程：
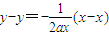与y=ax2
联立得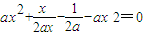
，
∴
，
，
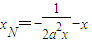易得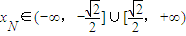
即xN取值范围是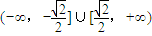
；（6分）
（Ⅱ）由题意得l的方程y-y=2ax（x-x），令y=0得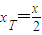
，∴
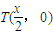
此时T到直线n的距离为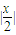
，又MF方程：
，
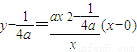设T到MF距离为d，则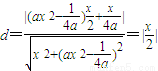
，
∴∠TMK=∠FMT，∴∠SMK=∠FMN．（13分）
点评：本题主要考查了抛物线的标准方程、直线与圆锥曲线的综合问题．直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现，主要涉及位置关系的判定，弦长问题、最值问题、对称问题、轨迹问题等，突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法．
（Ⅱ）欲证∠SMK=∠FMN，即要证∠TMK=∠FMT，为了证角相等，只要证明直线n是∠FMK的平分线，故只要证明T到直线n和直线MF距离相等即可．
解答：
解：（Ⅰ）易得直线m的方程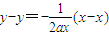：与y=ax2联立得
，∴
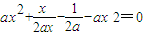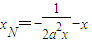，，易得
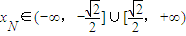
即xN取值范围是
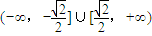；（6分）（Ⅱ）由题意得l的方程y-y=2ax（x-x），令y=0得
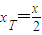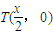
，∴此时T到直线n的距离为
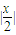，又MF方程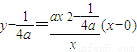：，设T到MF距离为d，则
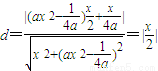，∴∠TMK=∠FMT，∴∠SMK=∠FMN．（13分）
点评：本题主要考查了抛物线的标准方程、直线与圆锥曲线的综合问题．直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现，主要涉及位置关系的判定，弦长问题、最值问题、对称问题、轨迹问题等，突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法．
练习册系列答案
相关题目
