题目内容

设集合A={(x，y)|
x2
4
+
y2
16
=1}，B={（x，y）|y=3x}，则A∩B的子集的个数是（　　）
A、4B、3C、2D、1
分析：由题意集合A={(x，y)|
x2
4
+
y2
16
=1}，B={（x，y）|y=3x}，画出A，B集合所表示的图象，看图象的交点，来判断A∩B的子集的个数．
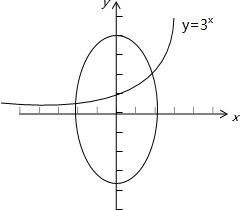解答：精英家教网解：∵集合A={(x，y)|
x2
4
+
y2
16
=1}，
∴
x2
4
+
y2
16
=1为椭圆和指数函数y=3x图象，
如图，可知其有两个不同交点，记为A1、A2，
则A∩B的子集应为∅，{A1}，{A2}，{A1，A2}共四种，
故选A．
点评：此题利用数形结合的思想来求解，主要考查集合和交集的定义及其运算法则，是一道不错的题．
练习册系列答案
相关题目
（理）设集合A={(x，y)|
y2
a2
-x2=1，a＞1}，B={(x，y)|y=tx，t＞
2a
，t≠1}，则A∩B的子集的个数是（　　）
A、4B、3C、2D、1
设集合A={x，y|y=ax+1}，B={x，y|y=|x|}，若A∩B的子集恰有2个，则实数a的取值范围是（　　）
设函数f（x）定义在R上，对于任意实数m、n，恒有f(m+n)=f(m)?f(n)，且当x＞0时，0＜f（x）＜1．
（1）求证：f（0）=1，且当x＜0时，f（x）＞1；
（2）设集合A={(x，y)|f(x2)?f(y2)＞f(1)}，B={（x，y）|f（ax-y+2）=1，a∈R}，若A∩B=∅，求a的取值范围．
（2013•宁波二模）设集合A={x，y|y=
4-x2
}，B={x，y|y=k（x-b）+1}，若对任意0≤k≤1都有A∩B≠∅，则实数b的取值范围是（　　）
设集合A={(x，y)|x2-
y2
36
=1}，B={(x，y)|y=3x}，则A∩B的子集的个数是（　　）
A、2B、4C、6D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网