题目内容
等差数列{an}中,Sn是其前n项和, =-2013,
=-2013,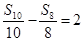 ,则
,则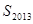 =
=
| A.-2012 | B.2013 | C.2012 | D.-2013 |
D
解析试题分析:因为Sn是等差数列的前n项和,所以 也为等差数列,其首项为-2013,公差2d=
也为等差数列,其首项为-2013,公差2d= ,所以
,所以 .
.
考点:等差数列的通项公式,前n项和公式,等差数列的定义.
点评:知道等差数列的前n项和公式是 ,从而可判断出
,从而可判断出 也为等差数列是解决此题的关键.
也为等差数列是解决此题的关键.

练习册系列答案
相关题目
已知 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,有下列四个命
,有下列四个命
题,假命题的是( )
A.公差 ; ; | B.在所有 中, 中, 最大; 最大; |
C.满足 的 的 的个数有11个; 的个数有11个; | D. ; ; |
在首项为57,公差为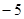 的等差数列
的等差数列 中,最接近零的是第( ) 项.
中,最接近零的是第( ) 项.
| A.14 | B.13 | C.12 | D.11 |
设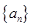 是等差数列,且
是等差数列,且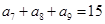 ,则其前15项和
,则其前15项和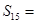 ( )
( )
| A.15 | B.45 | C.75 | D.105 |
数列 中,
中,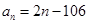 ,则使前n项和
,则使前n项和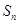 取得最小值的n的值为
取得最小值的n的值为
| A.52 | B.53 | C.54 | D.52或53 |
已知等差数列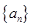 的通项公式
的通项公式 ,则
,则 等于 ( )
等于 ( )
| A.1 | B.2 | C.0 | D.9 |
在等差数列{ 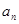 }中,
}中,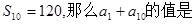 ( )
( )
| A.12 | B.24 | C.36 | D.48 |
如果-1,a,b,c,-9成等比数列,那么 ( )
| A.b=3,ac=9 | B.b=-3,ac=9 |
| C.b=3,ac=-9 | D.b=-3,ac=-9 |
在数列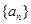 中,
中,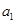 =1,
=1,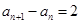 ,则
,则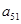 的值为( )
的值为( )
| A.99 | B.49 | C.102 | D.101 |