题目内容
数列 中,
中,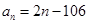 ,则使前n项和
,则使前n项和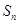 取得最小值的n的值为
取得最小值的n的值为
| A.52 | B.53 | C.54 | D.52或53 |
D
解析试题分析:由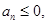 得
得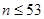 ,所以前n项和
,所以前n项和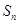 取得最小值的n的值为53或52.
取得最小值的n的值为53或52.
考点:等差数列的通项及前n项和公式.
点评:利用通项根据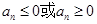 确定Sn的最小值或最大值.也可利用二次函数的性质直接研究Sn的最值即可.
确定Sn的最小值或最大值.也可利用二次函数的性质直接研究Sn的最值即可.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
设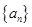 是等差数列,且
是等差数列,且 ,则这个数列的前5项和
,则这个数列的前5项和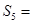 ( )
( )
| A.10 | B.15 | C.20 | D.25 |
已知等差数列 的前
的前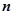 项和为
项和为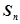 ,且满足
,且满足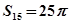 ,则
,则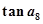 的值是( )
的值是( )
A. | B.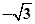 | C.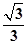 | D.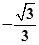 |
已知数列{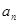 }中
}中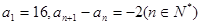 ,则数列
,则数列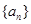 的前n项和
的前n项和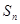 最大时,n的值为 ( )
最大时,n的值为 ( )
| A.8 | B.7或8 | C.8或9 | D.9 |
如果等差数列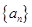 中,
中, ,那么
,那么
| A.14 | B.21 | C.28 | D.35 |
等差数列{an}中,Sn是其前n项和, =-2013,
=-2013,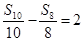 ,则
,则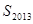 =
=
| A.-2012 | B.2013 | C.2012 | D.-2013 |
等差数列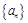 中,若
中,若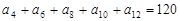 ,则
,则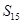 的值为: ( )
的值为: ( )
| A.180 | B.240 | C.360 | D.720 |
{an}是等差数列,且a1+a4+a7=45,a2+a5+a8=39,则a3+a6+a9的值是( )
| A.24 | B.27 | C.30 | D.33 |
已知 成等比数列,
成等比数列,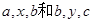 分别成等差数列,且
分别成等差数列,且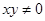 ,则
,则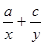 的值等于( )
的值等于( )
| A.1 | B.2 | C.3 | D.4 |