题目内容
在首项为57,公差为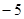 的等差数列
的等差数列 中,最接近零的是第( ) 项.
中,最接近零的是第( ) 项.
| A.14 | B.13 | C.12 | D.11 |
C
解析试题分析:根据首项为57,公差为-5的等差数列中,那么数列的通项公式为an=57+(n-1)(-5)=-5n+62,令an=0,得到5n=62,n=12.4,那么当n=12时,a12=2,a13=-3,a14=-8,可知最接近零的为第12项,故选C.
考点:本试题主要考查了等差数列的通项公式的运用。
点评:解决该试题的关键是利用首项和公差得到数列的通项公式,令通项公式为零,可知n的取值情况,来确定结论。

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
设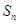 为等差数列{
为等差数列{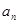 }的前n项和,若
}的前n项和,若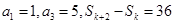 ,则k的值为
,则k的值为
| A.8 | B.7 | C.6 | D.5 |
在等差数列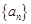 中,
中, ,则
,则 ( ).
( ).
| A.45 | B.75 | C.180 | D.300 |
已知等差数列 的前
的前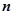 项和为
项和为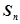 ,且满足
,且满足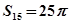 ,则
,则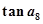 的值是( )
的值是( )
A. | B.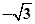 | C.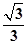 | D.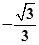 |
在等差数列 等于 ( )
等于 ( )
| A.22 | B.18 | C.20 | D.13 |
已知数列{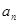 }中
}中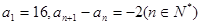 ,则数列
,则数列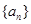 的前n项和
的前n项和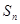 最大时,n的值为 ( )
最大时,n的值为 ( )
| A.8 | B.7或8 | C.8或9 | D.9 |
等差数列{an}中,Sn是其前n项和, =-2013,
=-2013,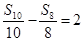 ,则
,则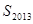 =
=
| A.-2012 | B.2013 | C.2012 | D.-2013 |
等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为 ( )
| A.130 | B.170 | C.210 | D.260 |
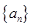 的前项和为
的前项和为 ,若
,若 三点共线,
三点共线, 为坐标原点,且
为坐标原点,且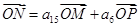 (直线
(直线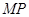 不过点
不过点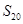 等于 ( )
等于 ( )