题目内容
由直角△ABC勾上一点D作弦AB的垂线交弦于E，交股的延长线于F，交外接圆于G，求证：EG为EA和EB的比例中项，又为ED和EF的比例中项．
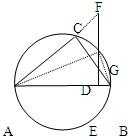
证明：连接GA、GB，
则△AGB也是一个直角三角形，
因为EG为直角△AGB的斜边AB上的高，
所以，EG为EA和EB的比例中项，
即EG2=EA?EB
∵∠AFE=∠ABC，
∴直角△AEF∽直角△DEB，
=
即EA?EB=ED?EF．
又∵EG2=EA?EB，
∴EG2=ED?EF（等量代换），
故EG也是ED和EF的比例中项．
则△AGB也是一个直角三角形，
因为EG为直角△AGB的斜边AB上的高，
所以，EG为EA和EB的比例中项，
即EG2=EA?EB
∵∠AFE=∠ABC，
∴直角△AEF∽直角△DEB，
| EA |
| EF |
| ED |
| EB |
又∵EG2=EA?EB，
∴EG2=ED?EF（等量代换），
故EG也是ED和EF的比例中项．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
如图，三棱锥P-ABC的顶点P在圆柱曲线O1O上，底面△ABC内接于⊙O的直径，且∠ABC=60°，O1O=AB=4，⊙O1上一点D在平面ABC上的射影E恰为劣弧AC的中点．
，求证：DO⊥平面PAC；
