题目内容
设函数f(x)=lnx-ax,a∈R.
(1)当x=1时,函数f(x)取得极值,求a的值;
(2)当a>0时,求函数f(x)在区间[1,2]的最大值;
(3)当a=-1时,关于x的方程2mf(x)=x2(m>0)有唯一实数解,求实数m的值.
解:(1)f(x)的定义域为(0,+∞),所以f′(x)= -a=
-a= . …(2分)
. …(2分)
因为当x=1时,函数f(x)取得极值,所以f′(1)=1-a=0,所以a=1.
经检验,a=1符合题意.(不检验不扣分) …(4分)
(2)f′(x)= -a=
-a= ,x>0.
,x>0.
令f′(x)=0得x= .因为x∈(0,
.因为x∈(0, )时,f′(x)>0,x∈(
)时,f′(x)>0,x∈( ,+∞)时,f′(x)<0,
,+∞)时,f′(x)<0,
所以f(x)在(0, )递增,在(
)递增,在( ,+∞)递减,…(5分)
,+∞)递减,…(5分)
①当0< ≤1,即a≥1时,f(x)在(1,2)上递减,所以x=1时,f(x)取最大值f(1)=-a;
≤1,即a≥1时,f(x)在(1,2)上递减,所以x=1时,f(x)取最大值f(1)=-a;
②当1< <2,即
<2,即 <a<1时,f(x)在(1,
<a<1时,f(x)在(1, )上递增,在(
)上递增,在(  ,2)上递减,
,2)上递减,
所以x= 时,f(x)取最大值f(
时,f(x)取最大值f( )=-lna-1;
)=-lna-1;
③当 ≥2,即0<a≤
≥2,即0<a≤ 时,f(x)在(1,2)上递增,所以x=2时,f(x)取最大值f(2)=ln2-2a.
时,f(x)在(1,2)上递增,所以x=2时,f(x)取最大值f(2)=ln2-2a.
综上,①当0<a≤ 时,f(x)最大值为ln2-2a;②当
时,f(x)最大值为ln2-2a;②当 <a<1时,f(x)最大值为-lna-1;
<a<1时,f(x)最大值为-lna-1;
③当a≥1时,f(x)最大值为-a. …(8分)
(每种情形1分)
(3)因为方程2mf(x)=x2有唯一实数解,
所以x2-2mlnx-2mx=0有唯一实数解,
设g(x)=x2-2mlnx-2mx,
则g′(x)=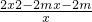 ,令g′(x)=0,x2-mx-m=0.
,令g′(x)=0,x2-mx-m=0.
因为m>0,x>0,所以x1=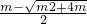 <0(舍去),x2=
<0(舍去),x2=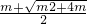 ,
,
当x∈(0,x2)时,g′(x)<0,g(x)在(0,x2)上单调递减,
当x∈(x2,+∞)时,g′(x)>0,g(x)在(x2,+∞)单调递增,
当x=x2时,g(x)取最小值g(x2). …(10分)
则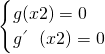
即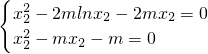
所以2mlnx2+mx2-m=0,因为m>0,所以2lnx2+x2-1=0(*),
设函数h(x)=2lnx+x-1,因为当x>0时,h(x)是增函数,所以h(x)=0至多有一解.
因为h(1)=0,所以方程(*)的解为x2=1,即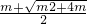 =1,
=1,
解得m= . …(12分)
. …(12分)
分析:(1)先求函数的定义域,然后求出导函数,根据f(x)在x=1处取得极值,则f'(1)=0,求出a的值,然后验证即可;
(2)先求出a的范围,然后利用导数研究函数的单调性,①当0< ≤1,即a≥1时,②当1<
≤1,即a≥1时,②当1< <2,③当
<2,③当 ≥2,分类讨论后,研究函数的单调性,从而求出函数f(x)在区间[1,2]的最大值;
≥2,分类讨论后,研究函数的单调性,从而求出函数f(x)在区间[1,2]的最大值;
(3)研究函数是单调性得到函数的极值点,根据函数图象的变化趋势,判断何时方程2mf(x)=x2有唯一实数解,得到m所满足的方程,解方程求解m.
点评:本题主要考查了利用导数研究函数的极值,以及利用导数研究函数在闭区间上的最值,是一道综合题,有一定的难度,属于中档题.
 -a=
-a= . …(2分)
. …(2分)因为当x=1时,函数f(x)取得极值,所以f′(1)=1-a=0,所以a=1.
经检验,a=1符合题意.(不检验不扣分) …(4分)
(2)f′(x)=
 -a=
-a= ,x>0.
,x>0.令f′(x)=0得x=
 .因为x∈(0,
.因为x∈(0, )时,f′(x)>0,x∈(
)时,f′(x)>0,x∈( ,+∞)时,f′(x)<0,
,+∞)时,f′(x)<0,所以f(x)在(0,
 )递增,在(
)递增,在( ,+∞)递减,…(5分)
,+∞)递减,…(5分)①当0<
 ≤1,即a≥1时,f(x)在(1,2)上递减,所以x=1时,f(x)取最大值f(1)=-a;
≤1,即a≥1时,f(x)在(1,2)上递减,所以x=1时,f(x)取最大值f(1)=-a;②当1<
 <2,即
<2,即 <a<1时,f(x)在(1,
<a<1时,f(x)在(1, )上递增,在(
)上递增,在(  ,2)上递减,
,2)上递减,所以x=
 时,f(x)取最大值f(
时,f(x)取最大值f( )=-lna-1;
)=-lna-1;③当
 ≥2,即0<a≤
≥2,即0<a≤ 时,f(x)在(1,2)上递增,所以x=2时,f(x)取最大值f(2)=ln2-2a.
时,f(x)在(1,2)上递增,所以x=2时,f(x)取最大值f(2)=ln2-2a.综上,①当0<a≤
 时,f(x)最大值为ln2-2a;②当
时,f(x)最大值为ln2-2a;②当 <a<1时,f(x)最大值为-lna-1;
<a<1时,f(x)最大值为-lna-1;③当a≥1时,f(x)最大值为-a. …(8分)
(每种情形1分)
(3)因为方程2mf(x)=x2有唯一实数解,
所以x2-2mlnx-2mx=0有唯一实数解,
设g(x)=x2-2mlnx-2mx,
则g′(x)=
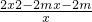 ,令g′(x)=0,x2-mx-m=0.
,令g′(x)=0,x2-mx-m=0.因为m>0,x>0,所以x1=
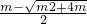 <0(舍去),x2=
<0(舍去),x2=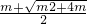 ,
,当x∈(0,x2)时,g′(x)<0,g(x)在(0,x2)上单调递减,
当x∈(x2,+∞)时,g′(x)>0,g(x)在(x2,+∞)单调递增,
当x=x2时,g(x)取最小值g(x2). …(10分)
则
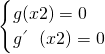
即
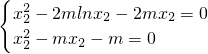
所以2mlnx2+mx2-m=0,因为m>0,所以2lnx2+x2-1=0(*),
设函数h(x)=2lnx+x-1,因为当x>0时,h(x)是增函数,所以h(x)=0至多有一解.
因为h(1)=0,所以方程(*)的解为x2=1,即
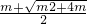 =1,
=1,解得m=
 . …(12分)
. …(12分)分析:(1)先求函数的定义域,然后求出导函数,根据f(x)在x=1处取得极值,则f'(1)=0,求出a的值,然后验证即可;
(2)先求出a的范围,然后利用导数研究函数的单调性,①当0<
 ≤1,即a≥1时,②当1<
≤1,即a≥1时,②当1< <2,③当
<2,③当 ≥2,分类讨论后,研究函数的单调性,从而求出函数f(x)在区间[1,2]的最大值;
≥2,分类讨论后,研究函数的单调性,从而求出函数f(x)在区间[1,2]的最大值;(3)研究函数是单调性得到函数的极值点,根据函数图象的变化趋势,判断何时方程2mf(x)=x2有唯一实数解,得到m所满足的方程,解方程求解m.
点评:本题主要考查了利用导数研究函数的极值,以及利用导数研究函数在闭区间上的最值,是一道综合题,有一定的难度,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目