题目内容

17．已知集合A={x|y=2|x|+1}，B={y|y=2|x|+1}，则A与B的关系是（　　）
A．A=BB．A∈BC．A∩B=BD．A∩B=∅

分析 根据条件求出集合A，B，利用A，B集合元素关系即可得到结论．

解答 解：A={x|y=2|x|+1}，A集合是研究函数y=x+1的定义域，故A=R
B={y|y=2|x|+1}，B集合是研究函数y=x+1的值域，故B={y|y≥1}
所以集合A与B的关系是：A∩B=B，
故选：C．

点评 本题主要考查集合的基本运算，属于基础题．要正确判断两个集合的关系，必须对集合的相关概念有深刻的理解，善于抓住代表元素，认清集合的特征．

练习册系列答案
相关题目
7．求函数y=$\frac{{x}^{2}-x+2}{x+1}$（x≠-1）的值域．
8．设（5x-$\frac{1}{\sqrt{x}}$）n的展开式的各项系数之和为M，二次项式系数之和为N，若M-N=56，则展开式中常数项为（　　）
A．-15B．15C．10D．-10
5．方程x2-1=3x的两根为x1，x2，则①x1+x2=3；②x1x2=-1；③$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-3；④x12+x22=11；⑤|x1-x2|=$\sqrt{13}$；⑥x12-3x1=1；⑦x2-$\frac{1}{{x}_{2}}$=3；⑧$\frac{1}{{{x}_{1}}^{3}}$+$\frac{1}{{x}_{2}^{3}}$=-36．
12．已知集合P={x|0≤x-a≤2}，Q={x|-3＜x≤4}，若P⊆Q，则a的取值范围是（-3，2]．
2．设函数f（x）=2x|x-a|+b（a＜0，b∈R），g（x）=x+1．
（1）讨论f（x）在[-1，1]上的单调性；
（2）当a=-1时，求函数h（x）=f（x）+b|g（-x）|在区间[-1，1]上的最小值．
9．已知p是q的必要不充分条件，则￢p是￢q的充分不必要条件．
6．若圆x2+y2-2x+2y+2-k2=0有且仅有两点到直线4x+3y-11=0的距离等于1，则正数k的取值范围为1＜k＜3．
7．如图，阴影部分可表示为（　　）
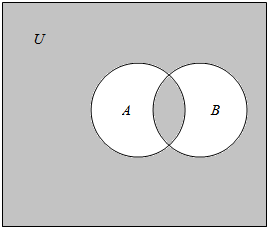
A．（A∪B）∩（∁U（A∩B））B．∁U（A∪B）C．∁U（A∩∁UB）D．[∁U（A∪B）]∪（A∩B）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网