题目内容
(2011•黑龙江一模)已知二面角α-l-β的平面角为θ,点P在二面角内,PA⊥α,PB⊥β,A,B为垂足,且PA=4,PB=5,设A,B到棱l的距离分别为x,y,当θ变化时,点(x,y)的轨迹方程是( )
分析:利用直角三角形的勾股定理得到(x,y)满足的方程,x,y的实际意义得到x,y都大于0据双曲线方程得到(x,y)的轨迹.
解答: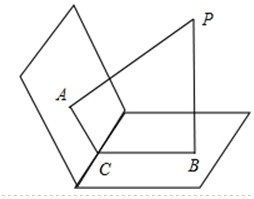 解:∵PA⊥α,PB⊥β,
解:∵PA⊥α,PB⊥β,
∴PB2+BC2=PA2+AC2
∴PB2+y2=PA2+x2
∵PA=4,PB=5,
∴x2-y2=9其中x≥0,y≥0.
故(x,y)轨迹为双曲线的右上支
故选B.
 解:∵PA⊥α,PB⊥β,
解:∵PA⊥α,PB⊥β,∴PB2+BC2=PA2+AC2
∴PB2+y2=PA2+x2
∵PA=4,PB=5,
∴x2-y2=9其中x≥0,y≥0.
故(x,y)轨迹为双曲线的右上支
故选B.
点评:本小题主要考查二面角、点的轨迹、圆锥曲线的定义等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011•黑龙江一模)已知三棱柱ABC-A1B1C1,底面三角形ABC为正三角形,侧棱AA1⊥底面ABC,AB=2,AA1=4,E为AA1的中点,F为BC中点.
(2011•黑龙江一模)已知三棱柱ABC-A1B1C1,底面三角形ABC为正三角形,侧棱AA1⊥底面ABC,AB=2,AA1=4,E为AA1的中点,F为BC中点. (2011•黑龙江一模)已知三棱柱ABC-A1B1C1,底面三角形ABC为正三角形,侧棱AA1⊥底面ABC,AB=2,AA1=4,E为AA1的中点,F为BC中点.
(2011•黑龙江一模)已知三棱柱ABC-A1B1C1,底面三角形ABC为正三角形,侧棱AA1⊥底面ABC,AB=2,AA1=4,E为AA1的中点,F为BC中点. (2011•黑龙江一模)阅读如图所示的程序框图,若输入p=5,q=6,则输出a,i的值分别为( )
(2011•黑龙江一模)阅读如图所示的程序框图,若输入p=5,q=6,则输出a,i的值分别为( )