题目内容
(本小题满分12分)
已知函数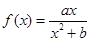 在
在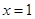 处取得极值为2,设函数
处取得极值为2,设函数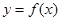 图象上任意一点
图象上任意一点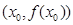 处的切线斜率为k。
处的切线斜率为k。
(1)求k的取值范围;
(2)若对于任意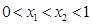 ,存在k,使得
,存在k,使得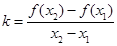 ,求证:
,求证: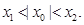
已知函数
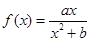 在
在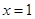 处取得极值为2,设函数
处取得极值为2,设函数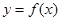 图象上任意一点
图象上任意一点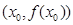 处的切线斜率为k。
处的切线斜率为k。(1)求k的取值范围;
(2)若对于任意
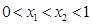 ,存在k,使得
,存在k,使得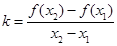 ,求证:
,求证: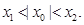
(Ⅰ)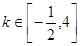 ;(Ⅱ)
;(Ⅱ)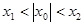 成立 。
成立 。
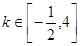 ;(Ⅱ)
;(Ⅱ)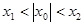 成立 。
成立 。本试题主要是考查了导数在研究函数中的运用。
(1)中,函数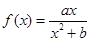 在
在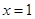 处取得极值为2那么可知道a,b的值,求解得到解析式。然后分析范围
处取得极值为2那么可知道a,b的值,求解得到解析式。然后分析范围
(2)根据由于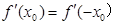 ,故只需要证明
,故只需要证明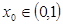 时结论成立
时结论成立
由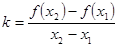 ,得
,得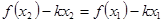 ,构造函数的思想,利用导数来得到证明。
,构造函数的思想,利用导数来得到证明。
解:(Ⅰ)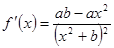
由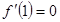 及
及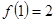 得,
得,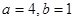 (2分)
(2分)
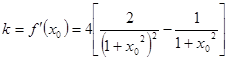
设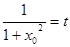 ,
,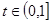 得
得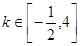 (4分)
(4分)
(Ⅱ)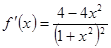 ,令
,令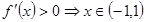
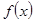 的增区间为
的增区间为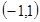 ,故当
,故当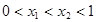 时,
时, .
.
即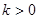 ,故
,故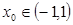 (6分)
(6分)
(法一)由于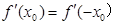 ,故只需要证明
,故只需要证明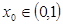 时结论成立
时结论成立
由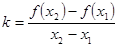 ,得
,得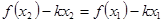 ,
,
记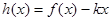 ,则
,则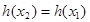
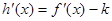 ,则
,则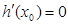 ,
,
设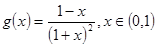 ,
,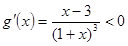 ,
,
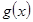 为减函数,故
为减函数,故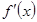 为减函数
为减函数
故当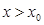 时有
时有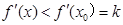 ,此时
,此时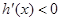 ,
,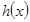 为减函数
为减函数
当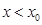 时
时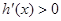 ,
,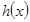 为增函数
为增函数
所以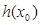 为
为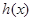 的唯一的极大值,因此要使
的唯一的极大值,因此要使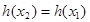 ,必有
,必有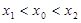
综上,有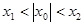 成立 (12分)
成立 (12分)
(法二) 由已知: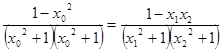 ①
①
下面以反证法证明结论:
假设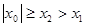 ,则
,则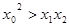 ,
,
因为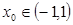 ,
,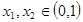 ,所以
,所以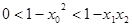 ,
,
又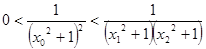 ,故
,故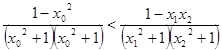
与①式矛盾
假设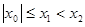 ,同理可得
,同理可得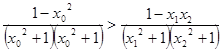
与①式矛盾
综上,有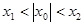 成立 (12分)
成立 (12分)
(1)中,函数
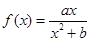 在
在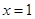 处取得极值为2那么可知道a,b的值,求解得到解析式。然后分析范围
处取得极值为2那么可知道a,b的值,求解得到解析式。然后分析范围(2)根据由于
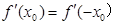 ,故只需要证明
,故只需要证明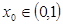 时结论成立
时结论成立由
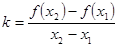 ,得
,得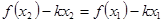 ,构造函数的思想,利用导数来得到证明。
,构造函数的思想,利用导数来得到证明。解:(Ⅰ)
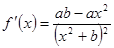
由
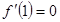 及
及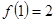 得,
得,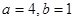 (2分)
(2分)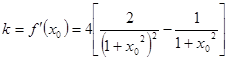
设
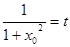 ,
,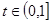 得
得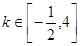 (4分)
(4分)(Ⅱ)
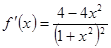 ,令
,令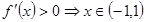
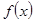 的增区间为
的增区间为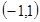 ,故当
,故当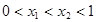 时,
时, .
.即
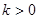 ,故
,故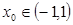 (6分)
(6分)(法一)由于
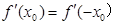 ,故只需要证明
,故只需要证明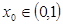 时结论成立
时结论成立由
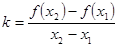 ,得
,得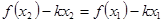 ,
,记
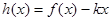 ,则
,则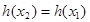
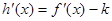 ,则
,则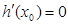 ,
,设
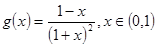 ,
,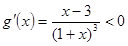 ,
,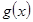 为减函数,故
为减函数,故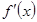 为减函数
为减函数故当
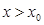 时有
时有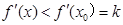 ,此时
,此时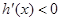 ,
,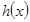 为减函数
为减函数当
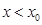 时
时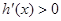 ,
,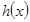 为增函数
为增函数所以
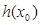 为
为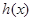 的唯一的极大值,因此要使
的唯一的极大值,因此要使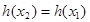 ,必有
,必有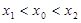
综上,有
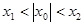 成立 (12分)
成立 (12分)(法二) 由已知:
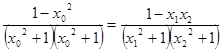 ①
①下面以反证法证明结论:
假设
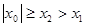 ,则
,则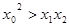 ,
,因为
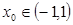 ,
,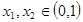 ,所以
,所以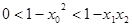 ,
,又
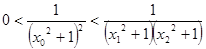 ,故
,故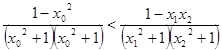
与①式矛盾
假设
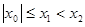 ,同理可得
,同理可得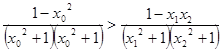
与①式矛盾
综上,有
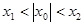 成立 (12分)
成立 (12分)
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由. .
. 在
在 的单调性;
的单调性; 为
为 上的最大值,写出
上的最大值,写出 ,
, 为f(x)的导函数,令a=- ,b=log32,则下列关系正确的是( )
为f(x)的导函数,令a=- ,b=log32,则下列关系正确的是( )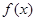 的导函数
的导函数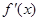 满足
满足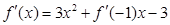 ,且
,且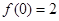 ,又
,又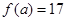 ,
,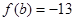 ,则
,则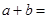 ( )
( ) 则
则 =__________________。
=__________________。 的导数是( )
的导数是( )



 ,若
,若 ,则
,则 ( )
( )



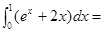 .
.