Question

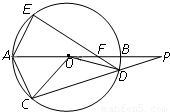
A．如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．求证：△PDF∽△POC．
B．已知矩阵A=

.

1 -2 3 -7

.

．
（1）求逆矩阵A^-1；
（2）若矩阵X满足AX=

3 1

，试求矩阵X．
C．坐标系与参数方程
已知极坐标系的极点O与直角坐标系的原点重合，极轴与x轴的正半轴重合，曲线C₁：ρcos（θ+

π

4

）=2

2

与曲线C₂：

x=4t2 y=4t

，（t∈R）交于A、B两点．求证：OA⊥OB．
D．已知x，y，z均为正数，求证：

x

yz

+

y

zx

+

z

xy

≥

1

x

+

1

y

+

1

z

．

Answer 1

分析：A、证明△PDF∽△POC，由于有公共角∠P，证明∠PFD=∠OCP即可；
B．（1）设A^-1=

a b c d

，利用A^-1A=E，即可求得；（2）利用（1）的逆矩阵可求；
C、先将极坐标方程化为普通方程，再将这两个方程联立，消去x，得y²-4y-16=0，再由韦达定理研究；
D、利用基本不等式证明

x

yz

+

y

zx

=

1

z

(

x

y

+

y

x

)≥

2

z

，

z

xy

+

y

zx

≥

2

x

，

z

xy

+

x

yz

≥

2

y

，即可证得结论．

解答：A、证明：∵AE=AC，∠CDE=∠AOC，
又∠CDE=∠P+∠PFD，∠AOC=∠P+∠OCP，
∴∠PFD=∠OCP
在△PDF与△POC中，∠P=∠P，∠PFD=∠OCP，∴△PDF∽△POC；
B．解：（1）设A^-1=

a b c d

，则

a b c d

1 -2 3 -7

=

a+3b -2a-7b c+3d -2c-7d

=

1 0 0 1

．
∴

a+3b=1 -2a-7b=0 c+3d=0 -2c-7d=1

，解得

a=7 b=-2 c=3 d=-1

，∴A^-1=

7 -2 3 -1

．
（2）X=

7 -2 3 -1

3 1

=

19 8

．
C．证明：曲线C₁的直角坐标方程x-y=4，曲线C₂的直角坐标方程是抛物线y²=4x，
设A（x₁，y₁），B（x₂，y₂），将这两个方程联立，消去x，得y²-4y-16=0
∴y₁y₂=-16，y₁+y₂=4，
∴x₁x₂+y₁y₂=（y₁+4）（y₂+4）+y₁y₂=2y₁y₂+4（y₁+y₂）+16=0
∴

OA

•

OB

=0，∴OA⊥OB
D． 证明：因为x，y，z都是为正数，所以

x

yz

+

y

zx

=

1

z

(

x

y

+

y

x

)≥

2

z

同理可得

z

xy

+

y

zx

≥

2

x

，

z

xy

+

x

yz

≥

2

y

，当且仅当x=y=z时，以上三式等号都成立
将上述三个不等式两边分别相加，并除以2，得

x

yz

+

y

zx

+

z

xy

≥

1

x

+

1

y

+

1

z

点评：本题考查选讲内容，考查知识点多，综合性强，用到知识多，属于中档题．