题目内容
【题目】如图所示,四边形ABCD是直角梯形,![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() .
.

![]() 求SC与平面ASD所成的角余弦值;
求SC与平面ASD所成的角余弦值;
![]() 求平面SAB和平面SCD所成角的余弦值.
求平面SAB和平面SCD所成角的余弦值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)建立直角坐标系,求出![]() 和平面ASD的一个法向量,设SC与平面ASD所成的角为θ,利用向量法求解即可;
和平面ASD的一个法向量,设SC与平面ASD所成的角为θ,利用向量法求解即可;
(2)分别求出平面SAB和平面SCD的法向量,利用向量法求解平面SAB和平面SCD所成角的余弦值.
(1)建立如图所示的空间直角坐标系,S(0,0,2),C(2,2,0),D(1,0,0),![]() =(2,2,﹣2),∵AB⊥平面SAD,故平面ASD的一个法向量为
=(2,2,﹣2),∵AB⊥平面SAD,故平面ASD的一个法向量为![]() =(0,2,0),设SC与平面ASD所成的角为θ,则sinθ=
=(0,2,0),设SC与平面ASD所成的角为θ,则sinθ=![]() =
=![]() =
=![]() ,故cosθ=
,故cosθ=![]() ,即SC与平面ASD所成的角余弦为:
,即SC与平面ASD所成的角余弦为:![]() .
.
(2)平面SAB的一个法向量为:![]() =(1,0,0),∵
=(1,0,0),∵![]() =(2,2,﹣2),
=(2,2,﹣2),![]() =(1,0,﹣2),设平面SCD的一个法向量为
=(1,0,﹣2),设平面SCD的一个法向量为![]() =(x,y,z),由
=(x,y,z),由![]()
![]() ,令z=1可得平面SCD的一个法向量为
,令z=1可得平面SCD的一个法向量为![]() =(2,﹣1,1)显然,平面SAB和平面SCD所成角为锐角,不妨设为α,则cosα=
=(2,﹣1,1)显然,平面SAB和平面SCD所成角为锐角,不妨设为α,则cosα=![]() =
=![]() ,即平面SAB和平面SCD所成角的余弦值为
,即平面SAB和平面SCD所成角的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某市环保部门为了让全市居民认识到冬天烧煤取暖对空气![]() 数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数
数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数![]() 与空气
与空气![]() 数值不合格的天数
数值不合格的天数![]() 进行统计分析,得出下表数据:
进行统计分析,得出下表数据:
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
(1)以统计数据为依据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)求出的线性回归方程,预测该市烧煤取暖的天数为20时空气![]() 数值不合格的天数.
数值不合格的天数.
参考公式: ,
,![]() .
.
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
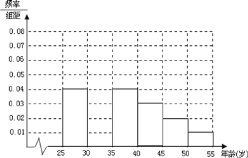
(1)补全频率分布直方图并求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)从![]() 岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动,如何抽取?
岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动,如何抽取?
