题目内容
已知函数f(x)=cos +2sin2x,x∈R.
+2sin2x,x∈R.
(1)求函数f(x)的最小正周期及对称轴方程;
(2)当x∈ 时,求函数f(x)的最大值和最小值及相应的x值.
时,求函数f(x)的最大值和最小值及相应的x值.
 +2sin2x,x∈R.
+2sin2x,x∈R.(1)求函数f(x)的最小正周期及对称轴方程;
(2)当x∈
 时,求函数f(x)的最大值和最小值及相应的x值.
时,求函数f(x)的最大值和最小值及相应的x值.(1)π,x= +
+ ,k∈Z(2)x=
,k∈Z(2)x= 时,f(x)max=2;x=0时,f(x)min=
时,f(x)max=2;x=0时,f(x)min=
 +
+ ,k∈Z(2)x=
,k∈Z(2)x= 时,f(x)max=2;x=0时,f(x)min=
时,f(x)max=2;x=0时,f(x)min=
(1)f(x)=cos +2sin2x=
+2sin2x= cos 2x+
cos 2x+ sin 2x+1-cos 2x=
sin 2x+1-cos 2x= sin 2x-
sin 2x- cos 2x+1=sin
cos 2x+1=sin +1.
+1.
则f(x)的最小正周期为T= =π.
=π.
由2x- =kπ+
=kπ+ ,得对称轴方程为x=
,得对称轴方程为x= +
+ ,k∈Z.
,k∈Z.
(2)当x∈ 时,-
时,- ≤2x-
≤2x- ≤
≤ ,
,
则当2x- =
= ,即x=
,即x= 时,f(x)max=2;
时,f(x)max=2;
当2x- =-
=- ,即x=0时,f(x)min=
,即x=0时,f(x)min=
 +2sin2x=
+2sin2x= cos 2x+
cos 2x+ sin 2x+1-cos 2x=
sin 2x+1-cos 2x= sin 2x-
sin 2x- cos 2x+1=sin
cos 2x+1=sin +1.
+1.则f(x)的最小正周期为T=
 =π.
=π.由2x-
 =kπ+
=kπ+ ,得对称轴方程为x=
,得对称轴方程为x= +
+ ,k∈Z.
,k∈Z.(2)当x∈
 时,-
时,- ≤2x-
≤2x- ≤
≤ ,
,则当2x-
 =
= ,即x=
,即x= 时,f(x)max=2;
时,f(x)max=2;当2x-
 =-
=- ,即x=0时,f(x)min=
,即x=0时,f(x)min=

练习册系列答案
相关题目
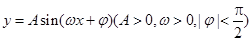 的最小值为
的最小值为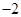 ,其图像相邻最高点与最低点横坐标之差为
,其图像相邻最高点与最低点横坐标之差为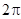 ,且图像过点(0,1),则其解析式是( )
,且图像过点(0,1),则其解析式是( )



 (
( )的最小正周期为
)的最小正周期为 .
. 的单调增区间;
的单调增区间; 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数 的图象.若
的图象.若 上至少含有
上至少含有 个零点,求
个零点,求 的最小值.
的最小值. 的图象如图所示,则f(0)=________.
的图象如图所示,则f(0)=________.
 cos(3x-θ)-sin(3x-θ)是奇函数,则θ为( )
cos(3x-θ)-sin(3x-θ)是奇函数,则θ为( ) (k∈Z)
(k∈Z) (k∈Z)
(k∈Z) ,
, )的图象的一条对称轴方程是( )
)的图象的一条对称轴方程是( )

 与函数g(x)=cos
与函数g(x)=cos ,下列说法正确的是( )
,下列说法正确的是( ) 对称
对称 则
则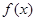 在区间[0,
在区间[0, ]上的最大值与最小值分别是( )
]上的最大值与最小值分别是( )