题目内容
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图).将矩形折叠,使A点落在线段DC上.(I)若折痕所在直线的斜率为k,试求折痕所在直线的方程;
(II)当
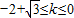 时,求折痕长的最大值;
时,求折痕长的最大值;(Ⅲ)当-2≤k≤-1时,折痕为线段PQ,设t=k(2|PQ|2-1),试求t的最大值.

【答案】分析:(1)分情况讨论斜率表示直线的方程
(2)表示出线段后,分类讨论求最值
(3)表示线段,用均值不等式求最值
解答:解: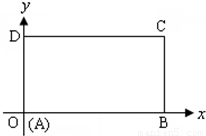 (1)①当k=0时,此时A点与D点重合,折痕所在的直线方程
(1)①当k=0时,此时A点与D点重合,折痕所在的直线方程
②当k≠0时,将矩形折叠后A点落在线段DC上的点记为G(a,1),
所以A与G关于折痕所在的直线对称,
有kOG•k=-1⇒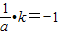 ⇒a=-k
⇒a=-k
故G点坐标为G(-k,1),
从而折痕所在的直线与OG的交点坐标
(线段OG的中点)为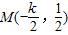
折痕所在的直线方程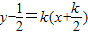 ,即
,即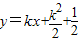
由①②得折痕所在的直线方程为: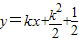
(2)当k=0时,折痕的长为2;
当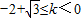 时,折痕直线交BC于点
时,折痕直线交BC于点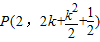 ,交y轴于
,交y轴于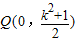
∵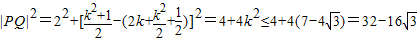
∴折痕长度的最大值为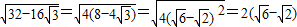
而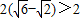
故折痕长度的最大值为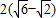
(3)当-2≤k≤-1时,折痕直线交DC于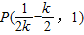 ,交x轴于
,交x轴于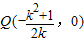
∵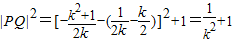
∴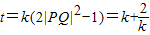
∵-2≤k≤-1
∴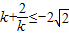 (当且仅当
(当且仅当 时取“=”号)
时取“=”号)
∴当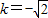 时,t取最大值,t的最大值是
时,t取最大值,t的最大值是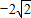 .
.
点评:本题考察内容比较综合,考察了求直线方程、求函数的最值、均值不等式、数形结合和分类讨论思想,属难题
(2)表示出线段后,分类讨论求最值
(3)表示线段,用均值不等式求最值
解答:解:
 (1)①当k=0时,此时A点与D点重合,折痕所在的直线方程
(1)①当k=0时,此时A点与D点重合,折痕所在的直线方程
②当k≠0时,将矩形折叠后A点落在线段DC上的点记为G(a,1),
所以A与G关于折痕所在的直线对称,
有kOG•k=-1⇒
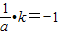 ⇒a=-k
⇒a=-k故G点坐标为G(-k,1),
从而折痕所在的直线与OG的交点坐标
(线段OG的中点)为
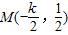
折痕所在的直线方程
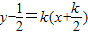 ,即
,即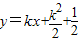
由①②得折痕所在的直线方程为:
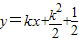
(2)当k=0时,折痕的长为2;
当
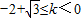 时,折痕直线交BC于点
时,折痕直线交BC于点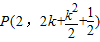 ,交y轴于
,交y轴于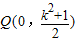
∵
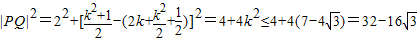
∴折痕长度的最大值为
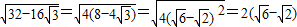
而
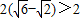
故折痕长度的最大值为
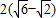
(3)当-2≤k≤-1时,折痕直线交DC于
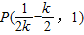 ,交x轴于
,交x轴于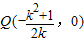
∵
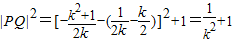
∴
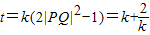
∵-2≤k≤-1
∴
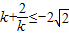 (当且仅当
(当且仅当 时取“=”号)
时取“=”号)∴当
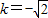 时,t取最大值,t的最大值是
时,t取最大值,t的最大值是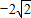 .
.点评:本题考察内容比较综合,考察了求直线方程、求函数的最值、均值不等式、数形结合和分类讨论思想,属难题

练习册系列答案
相关题目