题目内容
(本小题满分12分) 已知函数f (x) = ax2 + 2ln(1-x),其中a∈R.
(1)是否存在实数a,使得f (x)在x =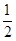 处取极值?若存在,求出a的值,若不存在,说明理由;
处取极值?若存在,求出a的值,若不存在,说明理由;
(2)若f (x)在[-1,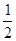 ]上是减函数,求实数a的取值范围.
]上是减函数,求实数a的取值范围.
(1)f (x)定义域为{x | x<1},f ′(x) = 2ax 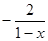
假设存在实数a,使f (x)在x =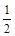 处取极值,则
处取极值,则
f ′(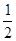 )
= a – 4 = 0, ∴a =
4
------------------ 3分
)
= a – 4 = 0, ∴a =
4
------------------ 3分
此时,f ′(x) = 8x 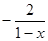 =
=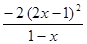
当x <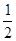 时,f ′(x) < 0;当
时,f ′(x) < 0;当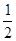 <x<1时,f ′(x) < 0.
<x<1时,f ′(x) < 0.
∴x =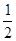 不是f (x)的极值点,
不是f (x)的极值点,
故不存在实数a,使f (x)在x =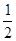 处极值 ------------- 6分
处极值 ------------- 6分
(2)解法一:依题意知:当x∈[-1,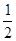 ]时,f ′(x) ≤0恒成立,
]时,f ′(x) ≤0恒成立,
f ′(x)≤0 2ax
–
2ax
– 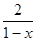 ≤0
≤0 ax≤
ax≤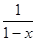
①当x = 0时,不等式显然成立;
②当-1≤x<0时,a≥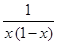
∵-1≤x<0
∴ x (1 – x) = – (x –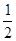 )2
+
)2
+ 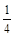 ∈
∈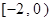
∴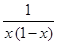 ≤
≤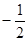 ∴a≥
∴a≥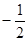 ------------- 9分
------------- 9分
③当0<x≤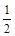 时,a≤
时,a≤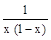
∵x∈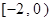 ,∴x (1 – x) = – (x –
,∴x (1 – x) = – (x –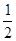 )2 +
)2 + 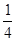 ∈
∈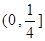
∴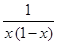 ≥4 ∴a≤4
≥4 ∴a≤4
综上可知,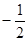 ≤a≤4为所求
---------------- 12分
≤a≤4为所求
---------------- 12分
解法二:依题意知:当x∈[-1,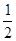 ]时,f ′(x) ≤0恒成立,
]时,f ′(x) ≤0恒成立,
f ′(x) ≤0 2ax
–
2ax
– 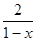 ≤0
≤0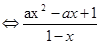 ≥0
≥0 ax2
– ax + 1≥0
ax2
– ax + 1≥0
令g (x) = ax2 – ax + 1 = a (x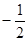 )2
+ 1
)2
+ 1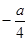 ,
x∈
,
x∈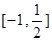
① 当a = 0时,g (x) = 1>0成立;
②当a>0时,g (x)在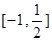 上递减,则
上递减,则
g (x)min = g (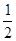 )
= 1
)
= 1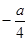 ≥0 ∴0<a≤4
------------ 9分
≥0 ∴0<a≤4
------------ 9分
③当a<0时,g (x)在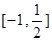 上递增,则
上递增,则
g (x)min = g (-1) = 2a + 1≥0 ∴0>a≥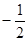
综上,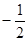 ≤a≤4为所求
-------------------- 12分
≤a≤4为所求
-------------------- 12分
【命题分析】本题主要考查运用导数研究函数性质的方法,分类讨论的数学思想和分析推理能力.
【解析】略

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案