题目内容
已知函数f（x）=
x2+lnx．
（I）求证：在区间[1，+∞）上，函数f（x）的图象在函数g（x）=
x3图象的下方；
（II）求证：[f′（x）]n-f′（xn）≥2n-2（n∈N*）．
证明：（I）设F（x）=x2+lnx-x3，则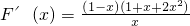
，
∵x＞1，∴F′（x）＜0，∴F（x）在[1，+∞）上是减函数．
又F（1）=-
＜0，故在[1，+∞）上，F（x）＜0，即x2+lnx＜x3，
∴在区间[1，+∞）上，函数f（x）的图象在函数g（x）=x3图象的下方；---------（6分）
（II）∵x＞0，∴[f′（x）]n-f′（xn）=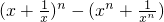
．
当n=1时，不等式显然成立；
当n≥2时，有[f′（x）]n-f′（xn）=
+
+…+
=[
+
+…+
]
≥（
+
+…+
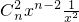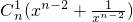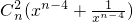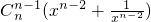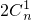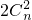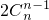）=2n-2
∴[f′（x）]n-f′（xn）≥2n-2（n∈N*）．--------------------（12分）
分析：（I）构造F（x）=x2+lnx-x3，利用导数确定在[1，+∞）上，F（x）＜0，即可得到结论；
（II）x＞0时，[f′（x）]n-f′（xn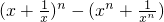）=，利用二项式定理，结合基本不等式，即可证得结论．
点评：本题考查导数知识的运用，考查函数的单调性，考查二项式定理的运用，考查学生分析解决问题的能力，属于中档题．
x2+lnx-x3，则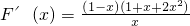，∵x＞1，∴F′（x）＜0，∴F（x）在[1，+∞）上是减函数．
又F（1）=-
＜0，故在[1，+∞）上，F（x）＜0，即x2+lnx＜x3，∴在区间[1，+∞）上，函数f（x）的图象在函数g（x）=
x3图象的下方；---------（6分）（II）∵x＞0，∴[f′（x）]n-f′（xn）=
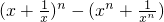．当n=1时，不等式显然成立；
当n≥2时，有[f′（x）]n-f′（xn）=
++…+=
[++…+]≥
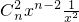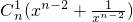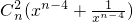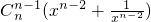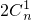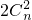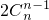（++…+）=2n-2∴[f′（x）]n-f′（xn）≥2n-2（n∈N*）．--------------------（12分）
分析：（I）构造F（x）=
x2+lnx-x3，利用导数确定在[1，+∞）上，F（x）＜0，即可得到结论；（II）x＞0时，[f′（x）]n-f′（xn）=
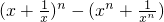，利用二项式定理，结合基本不等式，即可证得结论．点评：本题考查导数知识的运用，考查函数的单调性，考查二项式定理的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|