题目内容
8. 过圆外一点P作圆的切线PA(A为切点)再作割线PBC依次交圆于B,C,若PA=6,AB=4,BC=9,则AC=8.
过圆外一点P作圆的切线PA(A为切点)再作割线PBC依次交圆于B,C,若PA=6,AB=4,BC=9,则AC=8.
分析 由题意,∠PAB=∠C,可得△PAB∽△PCA,从而$\frac{PA}{PC}=\frac{PB}{PA}=\frac{AB}{CA}$,代入数据可得结果.
解答 解:由题意,∠PAB=∠C,∠APB=∠CPA,
∴△PAB∽△PCA,
∴$\frac{PA}{PC}=\frac{PB}{PA}=\frac{AB}{CA}$,
∵PA=6,AB=4,BC=9,
∴$\frac{6}{PB+9}$=$\frac{PB}{6}$=$\frac{4}{AC}$,
∴PB=3,AC=8,
故答案为:8.
点评 本题考查圆的切线的性质,考查三角形相似的判断,属于基础题.

练习册系列答案
相关题目
19.空间中,垂直于同一条直线的两条直线( )
| A. | 平行 | B. | 相交 | C. | 异面 | D. | 以上均有可能 |
17.已知圆C的圆心在y轴的负半轴上,且与x轴相切,被双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的渐近线截得的弦长为$\sqrt{3}$,则圆C的方程为( )
| A. | x2+(y+1)2=1 | B. | x2+(y+$\sqrt{3}$)2=3 | C. | x2+(y+$\frac{\sqrt{3}}{2}$)2=$\frac{3}{4}$ | D. | x2+(y+2)2=4 |
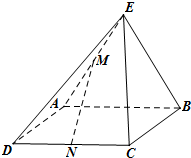 如图,矩形ABCD所在平面与直角三角形ABE所在平面互相垂直,AE⊥BE,点M,N分别是AE,CD的中点.
如图,矩形ABCD所在平面与直角三角形ABE所在平面互相垂直,AE⊥BE,点M,N分别是AE,CD的中点. 如图,四棱锥P-ABCD中,PD⊥平面ABCD,△ABD是边长为3的正三角形,BC=CD=$\sqrt{3}$,PD=4.
如图,四棱锥P-ABCD中,PD⊥平面ABCD,△ABD是边长为3的正三角形,BC=CD=$\sqrt{3}$,PD=4. 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),连结MC,MB,OT.
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),连结MC,MB,OT. 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=8,DC=4,则DE=2.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=8,DC=4,则DE=2.