题目内容
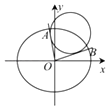
【题目】已知A、F分别是椭圆C： 
+ 
=1（a＞b＞0）的左顶点、右焦点，点P为椭圆C上一动点，当PF⊥x轴时，AF=2PF．
（1）求椭圆C的离心率；
（2）若椭圆C存在点Q，使得四边形AOPQ是平行四边形（点P在第一象限），求直线AP与OQ的斜率之积；
（3）记圆O：x2+y2= 
为椭圆C的“关联圆”．若b= 
，过点P作椭圆C的“关联圆”的两条切线，切点为M、N，直线MN的横、纵截距分别为m、n，求证： 
+ 
为定值．
【答案】
（1）
解：由PF⊥x轴，知xP=c，代入椭圆C的方程，
得： 
+ 
=1，解得 
，
又AF=2PF，∴a+c= 
，
∴a2+ac=2b2，即a2﹣2c2﹣ac=0，
∴2e2+e﹣1=0，
由e＞0解得椭圆C的离心率e= 
．
（2）
解：∵四边形AOPQ是平行四边形，∴PQ=a，且PF∥x轴，
∴ 
，代入椭圆C的方程，解得 
，
∵点P在第一象限，∴yp= 
b，
同理可得xQ=﹣ 
，yQ= b，
∴kAPkOQ= 
=﹣ 
，
由（1）知e= 
，得 = 
，∴kAPkOQ=﹣ ．
（3）
证明：由（1）知e= 
= ，又b= 
，解得a=2，
∴椭圆C的方程为 
=1，
圆O的方程为x2+y2= 
，①…
连接OM，ON，由题意可知，OM⊥PM，ON⊥PN，
∴四边形OMPN的外接圆是以OP 为直径的圆，
设P（x0，y0），则四边形OMPN的外接圆方程为（x﹣ 
）2+（y﹣ 
）2= 
（ 
），
即 
=0，②…
①﹣②，得直线MN的方程为xx0+yy0= ，
令y=0，则m= 
，令x=0，则n= 
．
∴ 
+ 
=49（ 
），
∵点P在椭圆C上，∴ 
+ 
=1，
∴ 
=49（为定值）．…
【解析】（1）由PF⊥x轴，知xP=c，代入椭圆C的方程，得 ，由此能求出椭圆C的离心率．（2）由四边形AOPQ是平行四边形，知PQ=a，且PF∥x轴，从而yp= b，yQ= b，由此能求出kAPkOQ ． （3）由（1）知e= = ，又b= ，从而椭圆C的方程为 =1，圆O的方程为x2+y2= ，连接OM，ON，由题意可知，OM⊥PM，ON⊥PN，从而四边形OMPN的外接圆是以OP 为直径的圆，由此能证明 为定值．
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
才能正确解答此题．
